5. Rational Functions

Graphing Rational Functions

5. Rational Functions

Graphing Rational Functions: Videos & Practice Problems

Topic summary

Understanding the graph of a rational function involves identifying key components such as vertical and horizontal asymptotes, x and y intercepts, and the function's domain. Transformations like shifts and reflections can modify the basic graph of $ \frac{1}{x} $. For example, a function like $ \frac{2x - 3}{x - 1} $ requires finding the domain by setting the denominator to zero, identifying intercepts, and determining asymptotic behavior based on the degrees of the numerator and denominator. This comprehensive approach allows for accurate graphing of rational functions.

concept

Graphing Rational Functions Using Transformations

Video duration:

Graphing Rational Functions Using Transformations Video Summary

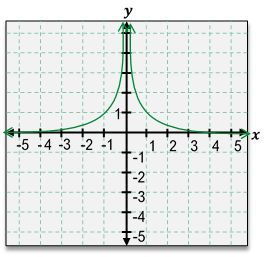
Understanding how to graph rational functions involves recognizing the fundamental components and applying transformations to them. A basic rational function, such as $ f(x) = \frac{1}{x} $, serves as a foundation for more complex graphs. By utilizing transformations, we can manipulate this basic function to create a new graph without performing extensive calculations.

Transformations of rational functions primarily include reflections and shifts. A negative sign outside the function indicates a reflection over the x-axis, while a negative sign inside the function reflects it over the y-axis. Horizontal shifts are represented by $ x - h $, where $ h $ indicates the number of units shifted left or right. Vertical shifts are denoted by $ + k $, indicating movement up or down by $ k $ units.

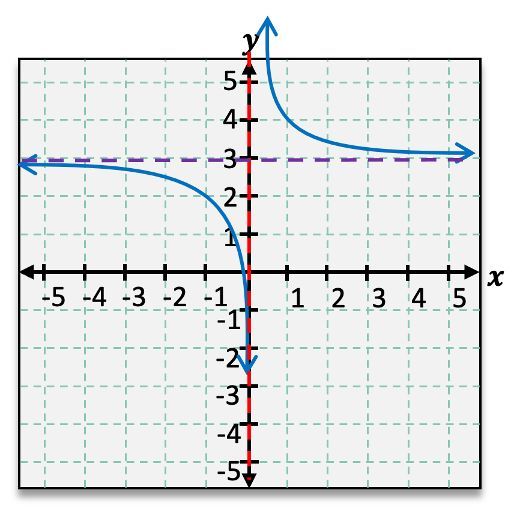
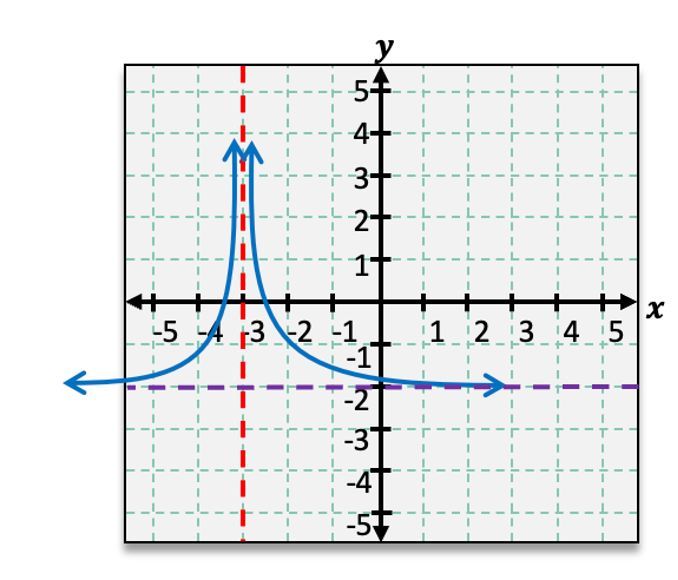
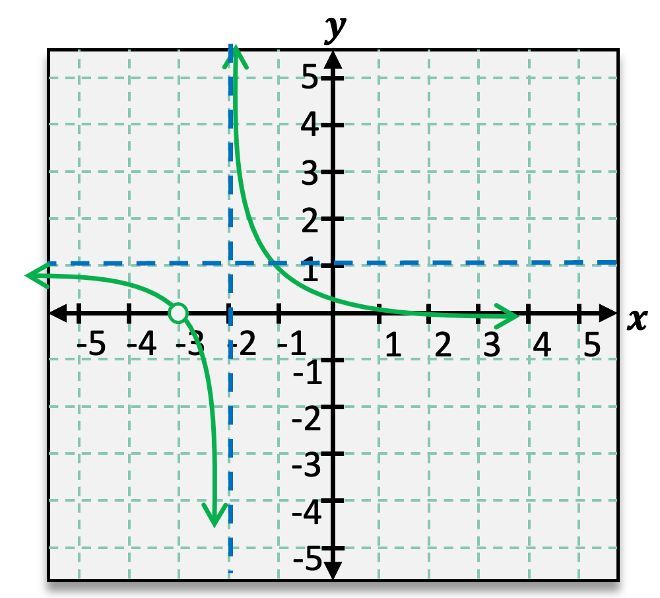
To graph a transformed function, such as $ g(x) = \frac{1}{x - 3} + 1 $, we start by identifying the vertical and horizontal asymptotes. The vertical asymptote is determined by the value of $ h $ in $ x - h $, which in this case is $ x = 3 $. The horizontal asymptote is found from $ k $, leading to $ y = 1 $. These asymptotes are plotted as dashed lines on the graph.

Next, we check for reflections. If there are no negative signs in the function, as in this example, we proceed without reflecting the graph. The next step involves shifting reference points based on the transformations. For instance, the point $ (1, 1) $ shifts 3 units to the right and 1 unit up, resulting in the new point $ (4, 2) $. Similarly, the point $ (-1, -1) $ shifts to $ (2, 0) $.

After plotting the transformed asymptotes and points, we sketch the curves approaching these asymptotes. The resulting graph will resemble the original $ \frac{1}{x} $ graph but will be repositioned according to the transformations applied.

Finally, we analyze the domain and range of the function. The domain is expressed in set notation, indicating intervals where the function is defined. For the function $ g(x) $, the domain is $ (-\infty, 3) \cup (3, \infty) $, reflecting the vertical asymptote at $ x = 3 $. The range follows a similar pattern, resulting in $ (-\infty, 1) \cup (1, \infty) $ due to the horizontal asymptote at $ y = 1 $. Both the domain and range exclude the asymptote values, hence the use of parentheses.

By mastering these transformation techniques, students can effectively graph rational functions and understand their behavior in relation to asymptotes, domain, and range.

Study Smarter with Worksheets.

Follow along with each video using our printable worksheets

example

Example 1

Video duration:

Example 1 Video Summary

To graph the function $ g(x) = -\frac{1}{(x - 2)^2} $, we start by recognizing that this is a transformation of the basic function $ f(x) = \frac{1}{x^2} $. The process involves several key steps to identify asymptotes, reflections, and shifts.

First, we determine the vertical asymptote, which occurs at $ x = h $. In this case, $ h = 2 $, so we plot a vertical dashed line at $ x = 2 $. Next, we identify the horizontal asymptote, represented by $ y = k $. Since there is no vertical shift in this function, $ k = 0 $, placing the horizontal asymptote at $ y = 0 $, which is consistent with the original function.

Next, we check for reflections in the graph. The negative sign in front of the function indicates a reflection over the x-axis. This means that points on the graph will be mirrored across the x-axis. For example, if we take the point $ (1, -1) $ from the original function, its reflection will be $ (1, 1) $. Similarly, the point $ (-1, -1) $ will reflect to $ (-1, 1) $.

After reflecting the points, we apply the horizontal and vertical shifts defined by $ h $ and $ k $. Since $ h = 2 $ and $ k = 0 $, we shift the reflected points 2 units to the right. The point $ (1, 1) $ shifts to $ (3, 1) $, and $ (-1, 1) $ shifts to $ (1, 1) $. This gives us our new points after reflection and shifting.

Now, we sketch the curve, ensuring it approaches the asymptotes. The shape of the graph will mirror that of the original function $ \frac{1}{x^2} $ but will be reflected and shifted accordingly. The resulting graph will approach the vertical asymptote at $ x = 2 $ and the horizontal asymptote at $ y = 0 $.

Finally, we identify the domain and range of the function. The domain is all real numbers except for the vertical asymptote, which can be expressed as $ (-\infty, 2) \cup (2, \infty) $. The range, due to the reflection, is limited to values below the x-axis, specifically $ (-\infty, 0) $.

In summary, the function $ g(x) = -\frac{1}{(x - 2)^2} $ features a vertical asymptote at $ x = 2 $, a horizontal asymptote at $ y = 0 $, and a range of $ (-\infty, 0) $ with a domain of $ (-\infty, 2) \cup (2, \infty) $.

Problem

Graph the rational function using transformations.
$f\left(x\right)=-\frac{1}{x}+3$

Graph of f(x) = -1/(x) + 3 showing vertical and horizontal asymptotes.

Graph of f(x) = -1/(x) + 3 with vertical and horizontal asymptotes.

Graph of f(x) = -1/(x) + 3 illustrating vertical and horizontal asymptotes.

Graph of f(x) = -1/(x) + 3 depicting vertical and horizontal asymptotes.

Problem

Graph the rational function using transformations.
$f\left(x\right)=\frac{1}{\left(x+3\right)^2}-2$

Graph of f(x)=1/(x+3)^2-2 showing vertical and horizontal asymptotes.

Graph of f(x)=1/(x+3)^2-2 with vertical asymptote at x=-3.

Graph of f(x)=1/(x+3)^2-2 illustrating behavior near vertical asymptote.

Graph of f(x)=1/(x+3)^2-2 showing a horizontal asymptote at y=-2.

concept

How to Graph Rational Functions

Video duration:

How to Graph Rational Functions Video Summary

Graphing a rational function involves several systematic steps to ensure accuracy. Let's consider the function $ f(x) = \frac{2x - 3}{x - 1} $ as an example to illustrate the process.

First, we need to determine the domain of the function. The domain is found by setting the denominator equal to zero. For our function, $ x - 1 = 0 $ leads to $ x = 1 $. Therefore, the domain is all real numbers except $ x = 1 $.

Next, we check for any holes in the graph by identifying common factors in the numerator and denominator. In this case, there are no common factors, so we can skip this step.

To find the x-intercepts, we set the numerator equal to zero: $ 2x - 3 = 0 $. Solving this gives $ x = \frac{3}{2} $ or $ 1.5 $. Since the factor occurs once, the multiplicity is 1, indicating that the graph will cross the x-axis at this point.

Next, we calculate the y-intercept by evaluating $ f(0) $:

$ f(0) = \frac{2(0) - 3}{0 - 1} = \frac{-3}{-1} = 3 $.

Thus, the y-intercept is at $ (0, 3) $.

Now, we find the vertical asymptote by setting the denominator equal to zero, which we already determined gives $ x = 1 $. This is represented on the graph as a dashed line.

For the horizontal asymptote, we compare the degrees of the numerator and denominator. Both have a degree of 1, so we divide the leading coefficients: $ \frac{2}{1} = 2 $. Therefore, the horizontal asymptote is at $ y = 2 $.

With the intercepts and asymptotes identified, we can now create intervals based on these points. The intervals are:

From $ -\infty $ to $ 1 $
From $ 1 $ to $ \frac{3}{2} $
From $ \frac{3}{2} $ to $ \infty $

Next, we select test points from each interval to determine the behavior of the function:

For the interval $ (-\infty, 1) $, choose $ x = -2 $: $ f(-2) = \frac{2(-2) - 3}{-2 - 1} = \frac{-4 - 3}{-3} = \frac{-7}{-3} = \frac{7}{3} \approx 2.33 $.
For the interval $ (1, \frac{3}{2}) $, choose $ x = \frac{5}{4} $: $ f\left(\frac{5}{4}\right) = \frac{2\left(\frac{5}{4}\right) - 3}{\frac{5}{4} - 1} = \frac{\frac{10}{4} - 3}{\frac{5}{4} - \frac{4}{4}} = \frac{\frac{10}{4} - \frac{12}{4}}{\frac{1}{4}} = \frac{-\frac{2}{4}}{\frac{1}{4}} = -2 $.
For the interval $ (\frac{3}{2}, \infty) $, choose $ x = 3 $: $ f(3) = \frac{2(3) - 3}{3 - 1} = \frac{6 - 3}{2} = \frac{3}{2} = 1.5 $.

Now we have the points $ (-2, \frac{7}{3}) $, $ \left(\frac{5}{4}, -2\right) $, and $ (3, 1.5) $ to plot on the graph. Finally, we connect these points while ensuring the graph approaches the asymptotes appropriately.

By following these steps, we can accurately sketch the graph of any rational function, capturing its key features such as intercepts, asymptotes, and overall behavior.

example

Example 1

Video duration:

10m

Example 1 Video Summary

To graph the rational function $ f(x) = \frac{2x^2}{x^2 - 1} $, we begin by determining the domain. The numerator $ 2x^2 $ does not factor further, while the denominator factors as $ (x + 1)(x - 1) $. Setting the denominator equal to zero, we find the restrictions: $ x \neq -1 $ and $ x \neq 1 $. Thus, the domain of the function excludes these values.

Next, we check for holes in the function by identifying any common factors between the numerator and denominator. Since there are no common factors, the function is already in its simplest form, indicating there are no holes.

To find the x-intercepts, we set the numerator equal to zero: $ 2x^2 = 0 $. Solving this gives $ x = 0 $. The multiplicity of this intercept is 2 (since it comes from $ 2x^2 $), indicating that the graph will touch the x-axis at this point but not cross it.

For the y-intercept, we evaluate $ f(0) $: $ f(0) = \frac{2(0)^2}{(0)^2 - 1} = 0 $. This confirms that the y-intercept is also at the origin, $ (0, 0) $.

Next, we identify vertical asymptotes by setting the denominator equal to zero, which yields the same restrictions as the domain: vertical asymptotes occur at $ x = -1 $ and $ x = 1 $.

To find the horizontal asymptote, we compare the degrees of the numerator and denominator. Both have a degree of 2, so we divide the leading coefficients: $ \frac{2}{1} = 2 $. Therefore, the horizontal asymptote is at $ y = 2 $.

Now, we divide the graph into intervals based on the asymptotes and intercepts: $ (-\infty, -1) $, $ (-1, 0) $, $ (0, 1) $, and $ (1, \infty) $. We select test points from each interval to evaluate the function:

For $ x = -3 $:
$ f(-3) = \frac{2(-3)^2}{(-3)^2 - 1} = \frac{18}{8} = \frac{9}{4} = 2.25 $ (point: $ (-3, 2.25) $)
For $ x = -\frac{1}{2} $:
$ f\left(-\frac{1}{2}\right) = \frac{2\left(-\frac{1}{2}\right)^2}{\left(-\frac{1}{2}\right)^2 - 1} = \frac{2 \cdot \frac{1}{4}}{\frac{1}{4} - 1} = \frac{\frac{1}{2}}{-\frac{3}{4}} = -\frac{2}{3} \approx -0.67 $ (point: $ \left(-\frac{1}{2}, -\frac{2}{3}\right) $)
For $ x = \frac{1}{2} $:
$ f\left(\frac{1}{2}\right) = -\frac{2}{3} $ (same as above, point: $ \left(\frac{1}{2}, -\frac{2}{3}\right) $)
For $ x = 2 $:
$ f(2) = \frac{2(2)^2}{(2)^2 - 1} = \frac{8}{3} \approx 2.67 $ (point: $ (2, 2.67) $)

After calculating these points, we plot them on the graph. The points are $ (-3, 2.25) $, $ \left(-\frac{1}{2}, -\frac{2}{3}\right) $, $ \left(\frac{1}{2}, -\frac{2}{3}\right) $, and $ (2, 2.67) $. We then connect these points while ensuring the graph approaches the vertical asymptotes at $ x = -1 $ and $ x = 1 $ and the horizontal asymptote at $ y = 2 $.

In summary, the graph of the function $ f(x) = \frac{2x^2}{x^2 - 1} $ features x-intercepts and y-intercepts at the origin, vertical asymptotes at $ x = -1 $ and $ x = 1 $, and a horizontal asymptote at $ y = 2 $. The behavior of the graph is characterized by touching the x-axis at the origin and approaching the asymptotes as described.

Problem

Graph the rational function.
$f\left(x\right)=\frac{x+3}{x^2+5x+6}$

Graph of f(x) = (x + 3) / (x^2 + 5x + 6) showing vertical and horizontal asymptotes.

Graph of f(x) = (x + 3) / (x^2 + 5x + 6) with two vertical asymptotes and a horizontal asymptote.

Graph of f(x) = (x + 3) / (x^2 + 5x + 6) showing a vertical asymptote at x = -3.

Graph of f(x) = (x + 3) / (x^2 + 5x + 6) with a vertical asymptote at x = -3 and a horizontal asymptote.

Do you want more practice?

More sets

Graphing Rational Functions

5. Rational Functions

5 problems

Topic

Justin

5. Rational Functions

3 topics 7 problems

Chapter

Callie

Go over this topic definitions with flashcards

More sets

Graphing Rational Functions definitions
5. Rational Functions
15 Terms

Here’s what students ask on this topic:

To graph a rational function using transformations, start with a basic function like $\frac{1}{x}$ . Identify any transformations such as shifts or reflections. For horizontal shifts, adjust the vertical asymptote to $x = h$ , and for vertical shifts, adjust the horizontal asymptote to $y = k$ . Check for reflections by looking for negative signs in the function. Shift key points by $(h, k)$ and sketch the curves approaching the asymptotes. The domain and range are split by the asymptotes and expressed in set notation. This method allows you to graph the function without detailed calculations, focusing on visual transformations.

To graph a complex rational function from scratch, begin by finding the domain by setting the denominator to zero. Identify x-intercepts by solving the numerator. Calculate the y-intercept by evaluating the function at $x =0$ . Determine vertical asymptotes by setting the denominator to zero and horizontal asymptotes by comparing the degrees of the numerator and denominator. Divide the graph into intervals based on vertical asymptotes and x-intercepts. Choose points within each interval, plot them, and connect the points, ensuring they approach the asymptotes. This comprehensive approach provides a detailed view of the function's behavior.

The domain of a rational function is found by identifying values of $x$ that make the denominator zero, as these values are not included in the domain. Set the denominator equal to zero and solve for $x$ . The domain is all real numbers except these values. For example, if the denominator is $x -1$ , set $x -1=0$ to find $x =1$ . The domain is all real numbers except $x =1$ , expressed as $(-ext{∞},1)igcup(1,ext{∞})$ .

Asymptotes are crucial in graphing rational functions as they indicate where the function approaches but never touches. Vertical asymptotes occur where the denominator is zero, showing undefined points. Horizontal asymptotes indicate the function's end behavior as $x$ approaches infinity. They guide the sketching of the graph, ensuring it approaches these lines without crossing them. Understanding asymptotes helps in accurately depicting the function's behavior and identifying its domain and range.

To find the x-intercepts of a rational function, set the numerator equal to zero and solve for $x$ . These are the points where the graph crosses the x-axis. For y-intercepts, evaluate the function at $x =0$ . This gives the point where the graph crosses the y-axis. For example, if the function is $\frac{2 x - 3}{x - 1}$ , set $2 x - 3 =0$ for x-intercepts and evaluate at $x =0$ for the y-intercept.