In the study of conic sections, the parabola is a unique shape that can be visualized by slicing a three-dimensional cone with a tilted plane. Understanding parabolas involves identifying two key components: the focus and the directrix. The focus is a specific point on the graph, while the directrix is a line. Both the focus and the directrix are equidistant from the vertex of the parabola, although they may be oriented in different directions.
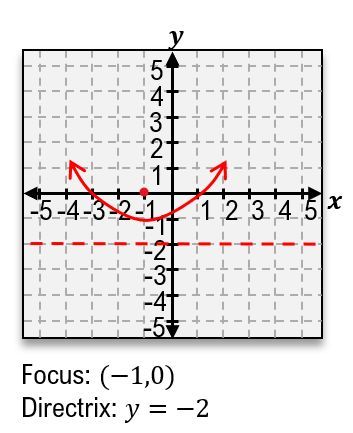
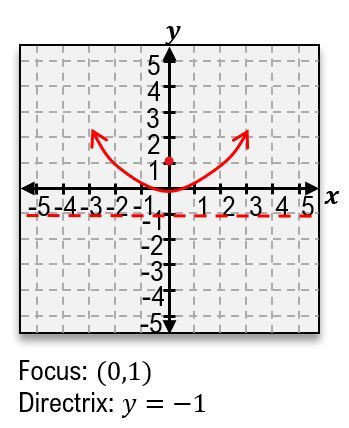
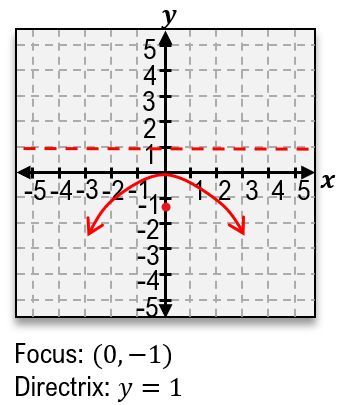
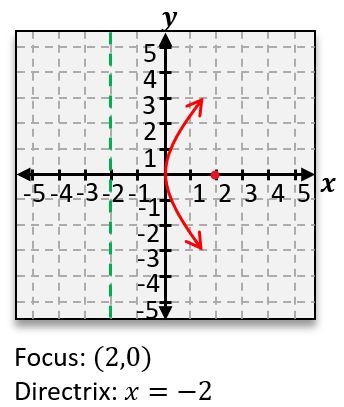
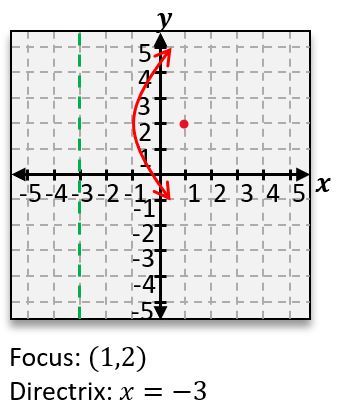
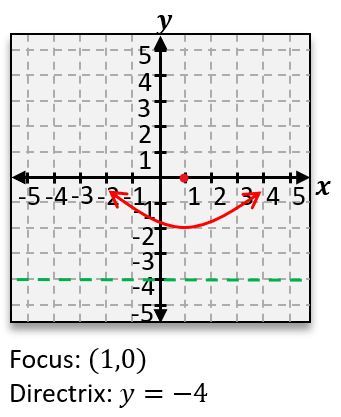
When analyzing a parabola, the orientation (opening upwards or downwards) determines the location of the focus and directrix. For a parabola that opens upwards, the focus is positioned above the vertex, while the directrix is below it. Conversely, if the parabola opens downwards, the focus is below the vertex, and the directrix is above it.
The standard form of a parabola's equation is crucial for finding the focus and directrix. The general equation can be expressed as:
\( y = \frac{1}{4p}(x - h)^2 + k \)
In this equation, \( (h, k) \) represents the vertex, and \( p \) is a value that indicates the distance from the vertex to the focus and the directrix. If the vertex is at the origin, the equation simplifies to:
\( y = \frac{1}{4p}x^2 \)
To find the value of \( p \), one can compare the coefficient of \( y \) in the equation to \( 4p \). For example, if \( 4p = 4 \), then \( p = 1 \). This means that for a parabola with a vertex at the origin, the focus would be located 1 unit above the vertex, and the directrix would be 1 unit below it.
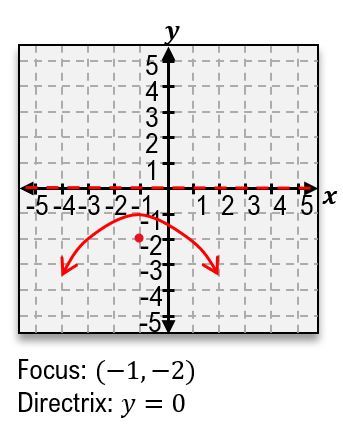
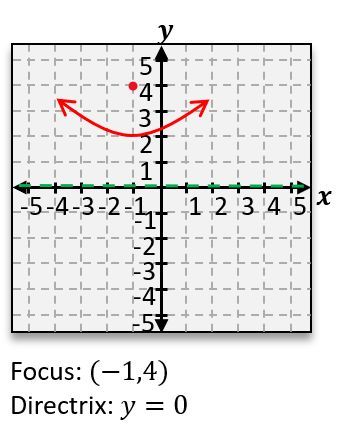
When given a specific parabola equation, the first step is to identify the vertex. For instance, if the equation is \( y - 2 = 2(x - 1)^2 \), the vertex can be determined as \( (1, 2) \). Next, the value of \( p \) can be calculated by recognizing that \( 4p = 8 \), leading to \( p = 2 \). This indicates that the focus is located 2 units above the vertex at the point \( (1, 4) \).
To determine the width of the parabola, one can move left and right from the focus by \( 2p \) units. In this case, moving 4 units from the focus gives points at \( (-3, 4) \) and \( (5, 4) \). Connecting these points with a smooth curve forms the parabola.
Finally, the directrix is found by moving down \( p \) units from the vertex. Since \( p = 2 \), the directrix is located at \( y = 0 \). This process illustrates how to effectively find the focus, directrix, and graph the parabola, enhancing understanding of this conic section.