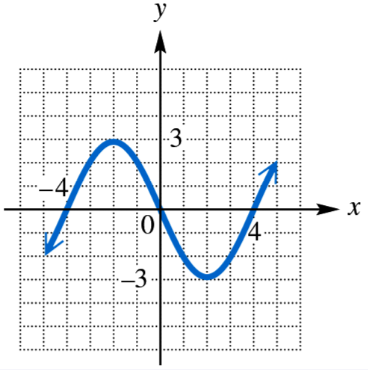
Determine whether each relation defines a function, and give the domain and range.

Verified step by step guidance

1. Step 1: Determine if the relation defines a function by using the Vertical Line Test. This test states that if any vertical line intersects the graph at more than one point, the relation is not a function.
2. Step 2: Observe the graph and check if any vertical line crosses the curve more than once. If no vertical line intersects the graph at multiple points, then the relation is a function.
3. Step 3: Identify the domain of the function by looking at the x-values covered by the graph. The domain includes all x-values from the leftmost point to the rightmost point on the graph.
4. Step 4: Identify the range of the function by looking at the y-values covered by the graph. The range includes all y-values from the lowest point to the highest point on the graph.
5. Step 5: Write the domain and range using interval notation, based on the minimum and maximum x and y values observed on the graph.

Key Concepts

Definition of a Function

A function is a relation where each input (x-value) corresponds to exactly one output (y-value). This means no vertical line intersects the graph more than once, ensuring each x has a unique y. Understanding this helps determine if a relation is a function by applying the vertical line test.

Domain of a Function

The domain is the set of all possible input values (x-values) for which the function is defined. On a graph, it corresponds to the horizontal extent of the curve. Identifying the domain involves finding the minimum and maximum x-values covered by the graph.

Range of a Function

The range is the set of all possible output values (y-values) that the function can produce. On a graph, it corresponds to the vertical extent of the curve. Determining the range involves identifying the lowest and highest points on the graph along the y-axis.