Textbook Question
In Exercises 9 - 16, find the following matrices: d. - 3A + 2B
67
views
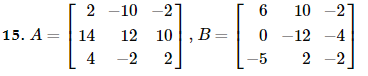
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:



 4:35m
4:35mMaster Introduction to Matrices with a bite sized video explanation from Patrick
Start learning