Determine whether each relation defines a function.
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
3. Functions
Intro to Functions & Their Graphs
Problem 21
Textbook Question
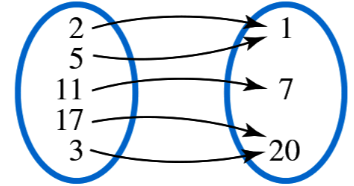
Determine whether each relation defines a function, and give the domain and range.
 Verified step by step guidance
Verified step by step guidance1
Step 1: Identify the domain and range from the diagram. The domain consists of the input values (left set): \(\{8, 14, 21, 27, 1\}\), and the range consists of the output values (right set): \(\{5, 13, 30\}\).
Step 2: Determine if the relation defines a function by checking if each element in the domain maps to exactly one element in the range. In the diagram, each domain value has exactly one arrow pointing to a single range value.
Step 3: Notice that the domain values 8 and 14 both map to 5, which is allowed in a function because different inputs can have the same output.
Step 4: Since no domain value maps to more than one range value, the relation is a function.
Step 5: Summarize the domain and range: Domain is \(\{8, 14, 21, 27, 1\}\) and Range is \(\{5, 13, 30\}\).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Function Definition
A function is a relation where each input (domain element) is paired with exactly one output (range element). This means no input can map to more than one output. Understanding this helps determine if a given relation qualifies as a function.
Recommended video:

Graphs of Common Functions
Domain and Range
The domain is the set of all possible inputs in a relation, while the range is the set of all possible outputs. Identifying these sets from a relation or mapping diagram is essential for analyzing the behavior and scope of the function.
Recommended video:

Domain & Range of Transformed Functions
Mapping Diagrams
Mapping diagrams visually represent relations by showing arrows from elements in the domain to elements in the range. They help easily identify if each domain element maps to one or multiple range elements, aiding in function verification.
Recommended video:

Probability of Mutually Exclusive Events

 5:2m
5:2mWatch next
Master Relations and Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
570
views
