Give a rule for each piecewise-defined function. Also give the domain and range.
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
3. Functions
Intro to Functions & Their Graphs
Problem 56
Textbook Question
Graph each function. Give the domain and range. g(x)=[[2x-1]]
 Verified step by step guidance
Verified step by step guidance1
Identify the function given: \(g(x) = \left\lfloor 2x - 1 \right\rfloor\), where \(\left\lfloor \cdot \right\rfloor\) denotes the floor function, which outputs the greatest integer less than or equal to the input.
Determine the domain of \(g(x)\). Since the expression inside the floor function, \$2x - 1$, is defined for all real numbers, the domain is all real numbers: \((-\infty, \infty)\).
To find the range, consider that the floor function outputs integers. As \(x\) varies over all real numbers, \$2x - 1\( takes all real values from \(-\infty\) to \(\infty\), so \)g(x)$ takes all integer values from \(-\infty\) to \(\infty\). Thus, the range is all integers: \(\{ ..., -2, -1, 0, 1, 2, ... \}\).
To graph \(g(x)\), note that for each integer \(k\), the function \(g(x) = k\) on the interval where \(k \leq 2x - 1 < k+1\). Solve these inequalities for \(x\) to find the intervals:
\[ \frac{k+1}{2} > x \geq \frac{k+1}{2} \]
Plot horizontal steps at each integer value \(k\) over the corresponding intervals on the \(x\)-axis, remembering that the graph is a step function with jumps at points where \$2x - 1$ is an integer.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
14mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Greatest Integer Function (Floor Function)
The greatest integer function, denoted by [[x]] or ⌊x⌋, maps any real number to the largest integer less than or equal to that number. For example, [[2.3]] = 2 and [[-1.7]] = -2. Understanding this function is essential for graphing g(x) = [[2x - 1]] because it creates a step-like graph.
Recommended video:

Function Composition
Domain and Range of Functions
The domain of a function is the set of all possible input values (x-values), while the range is the set of all possible output values (y-values). For g(x) = [[2x - 1]], the domain is all real numbers, but the range consists of all integers because the greatest integer function outputs integers only.
Recommended video:
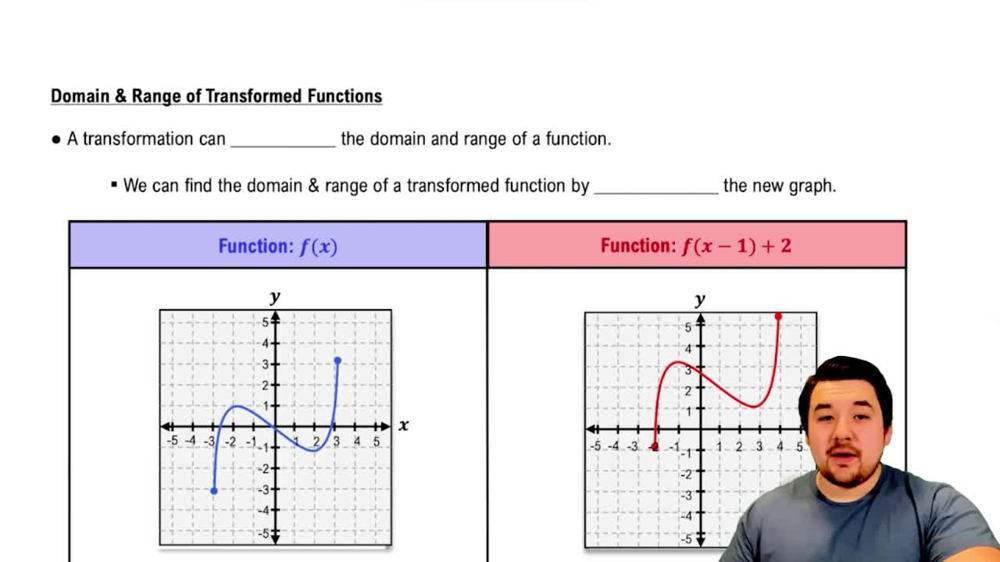
Domain & Range of Transformed Functions
Graphing Step Functions
Step functions like the greatest integer function produce graphs with horizontal segments and jumps at integer boundaries. When graphing g(x) = [[2x - 1]], each step corresponds to intervals where 2x - 1 lies between consecutive integers, resulting in a series of horizontal line segments with jumps at specific x-values.
Recommended video:
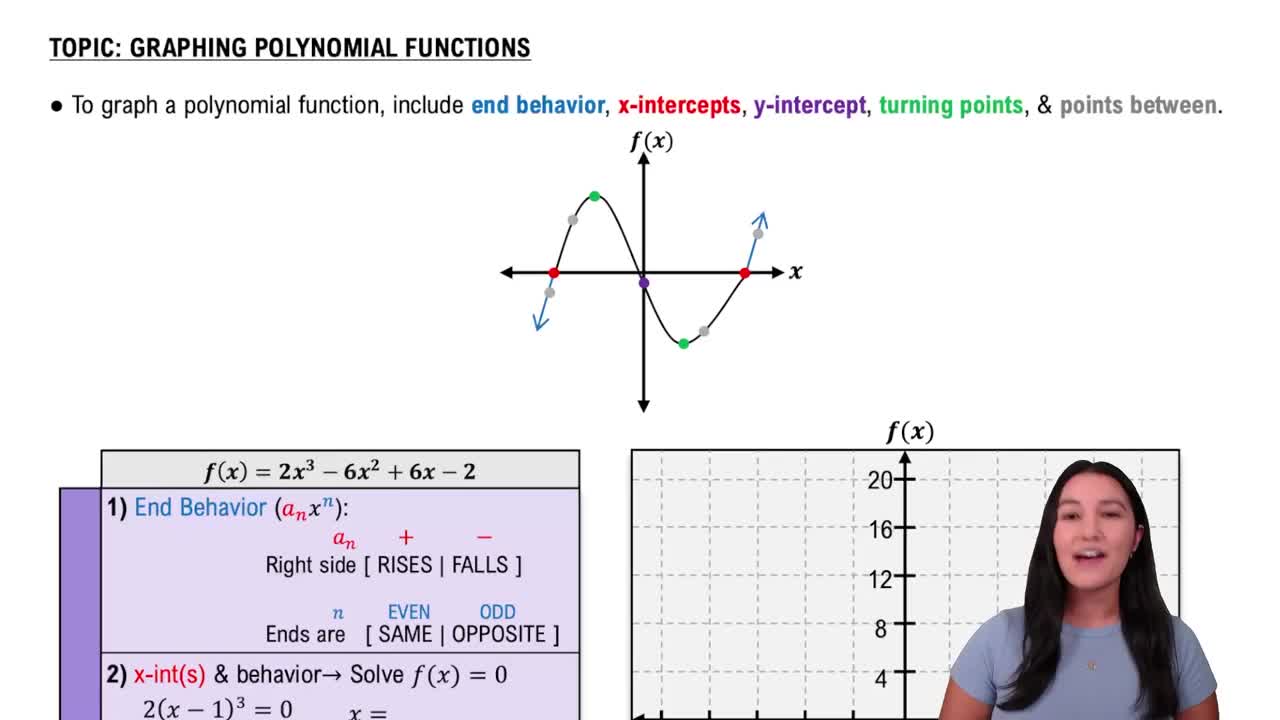
Graphing Polynomial Functions
Related Videos
Related Practice
Textbook Question
687
views


