In Exercises 19–24, the graph of an exponential function is given. Select the function for each graph from the following options: f ( x ) = 3 x , g ( x ) = 3 x − 1 , h ( x ) = 3 x − 1 , f ( x ) = − 3 x , G ( x ) = 3 − x , H ( x ) = − 3 − x . f(x) = 3^x, \quad g(x) = 3^{x-1}, \quad h(x) = 3^x - 1, \\f(x) = -3^x, \quad G(x) = 3^{-x}, \quad H(x) = -3^{-x}. f ( x ) = 3 x , g ( x ) = 3 x − 1 , h ( x ) = 3 x − 1 , f ( x ) = − 3 x , G ( x ) = 3 − x , H ( x ) = − 3 − x .

Hello. Today we're going to be figuring out the function for the given graph. So what we are given is this exponential function? Who's horizontal ascent tote is that Y is equal to zero and passes through the 00.1 comma six. So the general form of an exponential function is F. Of X. Is equal to some constant base be raised to the power of X. And looking at the given graph, there seems to be no transformations applied to the original function. So we're going to need to figure out what the base B is for a general function. Let's take a look at the 0.1 comma six. What this is saying is that if I plug in the value of one to our function this is going to spit out the value of six. So if I plug in the value of one to our general function we're going to get F of one is equal to B to the power of one which is equal to six. And we can go ahead and use this statement to solve our base B, B to the power of one is just going to give me B. So what I am left with is B is equal to six. And if I take this value and replace it for be in our general function, what I get is the function F. Of X is equal to six to the power of X. And this is going to be the function for the given graph. And with that being said, the answer to this problem is going to be be. So I hope this video helps you in understanding how to approach this problem, and I'll go ahead and see you all in the next video.

6. Exponential & Logarithmic Functions

Introduction to Exponential Functions

College Algebra

6. Exponential & Logarithmic Functions

Introduction to Exponential Functions

1:40 minutes

Problem 19

Textbook Question

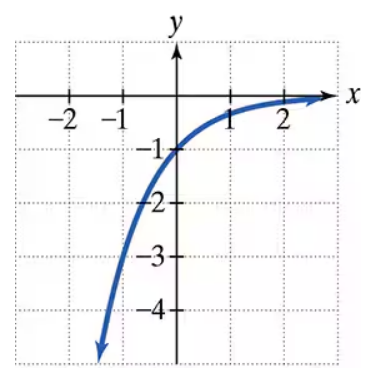
In Exercises 19–24, the graph of an exponential function is given. Select the function for each graph from the following options:
$f(x) = 3^x, \quad g(x) = 3^{x-1}, \quad h(x) = 3^x - 1, \\f(x) = -3^x, \quad G(x) = 3^{-x}, \quad H(x) = -3^{-x}.$

Verified step by step guidance

Step 1: Identify the general shape of the graph. The graph shows exponential growth, which means the base of the exponential function is greater than 1, and the function increases as x increases.

Step 2: Check the y-intercept of the graph. The y-intercept occurs when x = 0. From the graph, observe the value of the function at x = 0.

Step 3: Compare the y-intercept to the given functions. For example, for f(x) = 3^x, the y-intercept is 3^0 = 1. For g(x) = 3^(x-1), the y-intercept is 3^{-1} = 1/3. For h(x) = 3^x - 1, the y-intercept is 1 - 1 = 0.

Step 4: Look at the behavior of the graph for negative x-values. If the graph approaches zero but never touches the x-axis, it matches the behavior of 3^x or its transformations. If the graph is reflected or shifted, it will affect this behavior.

Step 5: Based on the y-intercept and the shape, match the graph to the correct function from the options: f(x) = 3^x, g(x) = 3^(x-1), h(x) = 3^x - 1, f(x) = -3^x, G(x) = 3^{-x}, or H(x) = -3^{-x}.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Exponential Functions

An exponential function has the form f(x) = a^x, where the base a is a positive constant not equal to 1. These functions exhibit rapid growth or decay depending on the base and the exponent's sign. Understanding the general shape and behavior of exponential graphs is essential for identifying specific functions.

Horizontal and Vertical Shifts

Shifts in exponential functions occur when constants are added or subtracted inside the exponent or outside the function. For example, f(x) = 3^(x-1) shifts the graph right by 1 unit, while f(x) = 3^x - 1 shifts it down by 1 unit. Recognizing these shifts helps match graphs to their corresponding equations.

Reflections and Negative Exponents

A negative sign in front of the function reflects the graph across the x-axis, while a negative exponent reflects it across the y-axis. For instance, f(x) = -3^x flips the graph vertically, and g(x) = 3^(-x) flips it horizontally. Identifying these reflections is key to distinguishing between similar exponential functions.

Watch next

Master Exponential Functions with a bite sized video explanation from Patrick

Start learning