Use vertices and asymptotes to graph each hyperbola. Locate the foci and find the equations of the asymptotes.
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
8. Conic Sections
Hyperbolas NOT at the Origin
Problem 1
Textbook Question
Find the vertices and locate the foci of each hyperbola with the given equation. Then match each equation to one of the graphs that are shown and labeled (a)–(d).
a.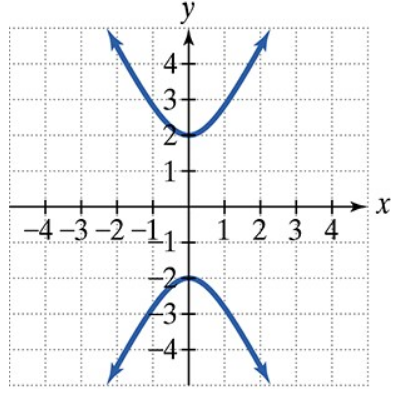 b.
b. 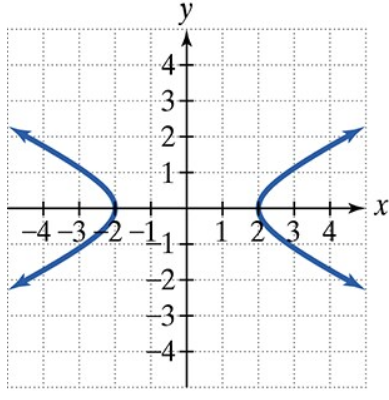 c.
c. 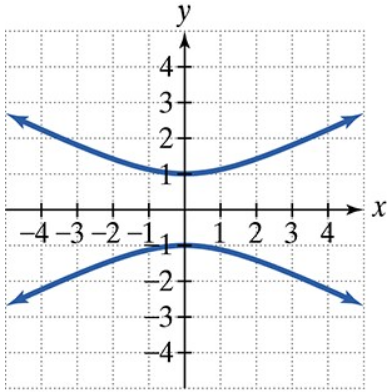 d.
d. 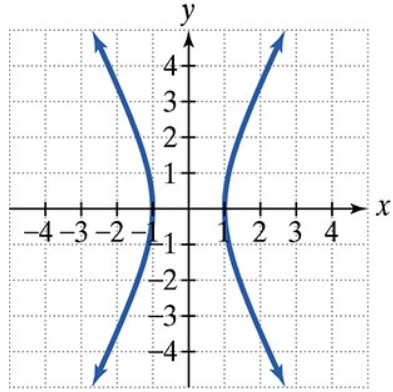
x2/4−y2/1=1
 Verified step by step guidance
Verified step by step guidance1
Identify the standard form of the hyperbola equation given: \(\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1\). Here, \(a^{2} = 4\) and \(b^{2} = 1\).
Find the vertices of the hyperbola. Since the \(x^{2}\) term is positive and comes first, the hyperbola opens left and right. The vertices are located at \((\pm a, 0)\), so calculate \(a = \sqrt{4}\).
Calculate the coordinates of the vertices using the value of \(a\). The vertices will be at \((\pm a, 0)\).
Find the foci of the hyperbola. Use the relationship \(c^{2} = a^{2} + b^{2}\) to find \(c\), where \(c\) is the distance from the center to each focus.
Calculate \(c = \sqrt{a^{2} + b^{2}}\) and then write the coordinates of the foci as \((\pm c, 0)\). Use these points to match the hyperbola to the correct graph among options (a)–(d).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Standard Form of a Hyperbola
A hyperbola's equation in standard form is either (x²/a²) - (y²/b²) = 1 or (y²/a²) - (x²/b²) = 1. This form helps identify the orientation (horizontal or vertical) and key parameters like a and b, which are essential for locating vertices and foci.
Recommended video:

Asymptotes of Hyperbolas
Vertices of a Hyperbola
Vertices are points where the hyperbola intersects its transverse axis. For the equation (x²/a²) - (y²/b²) = 1, vertices are at (±a, 0). Knowing the vertices helps in sketching the hyperbola and understanding its shape and size.
Recommended video:

Foci and Vertices of Hyperbolas
Foci of a Hyperbola
Foci are two fixed points used to define a hyperbola, located along the transverse axis at a distance c from the center, where c² = a² + b². Finding the foci is crucial for graphing and matching the hyperbola to its correct graph.
Recommended video:

Foci and Vertices of Hyperbolas

 5:59m
5:59mWatch next
Master Graph Hyperbolas NOT at the Origin with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
626
views
