Use the graphs of f and g to solve Exercises 83–90.

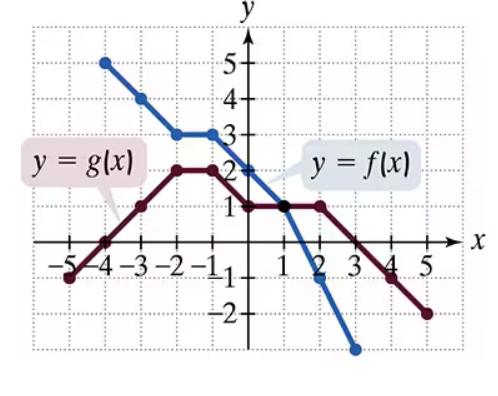
Find(g/f)(3)

Verified step by step guidance

1. Step 1: Understand the problem. You are tasked with finding (g/f)(3), which means you need to evaluate the function g(x) divided by f(x) at x = 3.
2. Step 2: Locate x = 3 on the graph. Look at the vertical line corresponding to x = 3 and identify the y-values of both f(x) (blue graph) and g(x) (red graph).
3. Step 3: Determine the value of g(3). From the graph, find the y-coordinate of the red graph at x = 3.
4. Step 4: Determine the value of f(3). From the graph, find the y-coordinate of the blue graph at x = 3.
5. Step 5: Divide g(3) by f(3). Use the values obtained in Steps 3 and 4 to compute g(3)/f(3). Ensure that f(3) is not zero to avoid division by zero.

Key Concepts

Function Notation

Function notation is a way to represent functions in mathematics, typically using symbols like f(x) and g(x). Here, f and g are functions, and x is the input variable. Understanding function notation is essential for interpreting and manipulating functions, especially when performing operations like addition, subtraction, multiplication, or division.

Graph Interpretation

Interpreting graphs involves analyzing the visual representation of functions to extract information about their behavior. In this case, the graphs of f(x) and g(x) provide insights into their values at specific points, such as x = 3. This skill is crucial for solving problems that require evaluating functions based on their graphical representations.

Division of Functions

The division of functions, denoted as (g/f)(x), represents the quotient of two functions g(x) and f(x). To find (g/f)(3), one must evaluate g(3) and f(3) from their respective graphs and then compute the ratio g(3)/f(3). This concept is fundamental in algebra as it allows for the exploration of relationships between different functions.