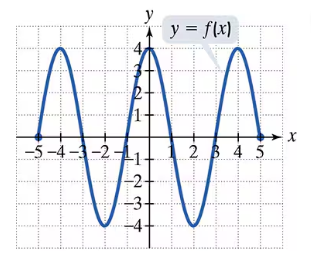
In Exercises 65–70, use the graph of f to find each indicated function value. f(4)

Verified step by step guidance

1. Identify the point on the graph where the input value (x) is 4.
2. Locate the vertical line corresponding to x = 4 on the x-axis.
3. Find the point on the curve of the function f(x) that intersects this vertical line.
4. Determine the y-coordinate of this intersection point, which represents the value of f(4).
5. Read the y-value from the graph at x = 4 without calculating, just noting the position on the y-axis.

Key Concepts

Function and Function Notation

A function assigns each input exactly one output. The notation f(x) represents the output value of the function f at the input x. Understanding this notation is essential to interpret and evaluate function values from graphs or equations.

Reading Values from a Graph

To find f(4) from a graph, locate the input value x = 4 on the x-axis, then find the corresponding point on the curve. The y-coordinate of this point is the function value f(4). This skill is crucial for interpreting graphical data.

Properties of Sinusoidal Functions

Sinusoidal functions, like sine and cosine, have wave-like patterns with regular peaks and troughs. Recognizing these patterns helps predict function values and understand periodic behavior, which is useful when analyzing graphs of such functions.