Solve the triangle: a=5a=5a=5, b=15b=15b=15, c=13c=13c=13.

A = 18.9 ° , B = 103.8 ° , C = 57.3 ° A=18.9\degree,B=103.8\degree,C=57.3\degree A = 18.9° , B = 103.8° , C = 57.3°

Solve the triangle : a = 5 a=5 a = 5 , b = 15 b=15 b = 15 , c = 13 c=13 c = 13 .

Hey, everyone. So in this triangle, we're given 3 values. We're given 3 lowercase letters, a, b, and c, and we're asked to solve it, which means we're gonna figure out all of the remaining information. So we actually don't even really have to do the first step, which is sketching the triangle because we already know what type of triangle we're dealing with. We're dealing with an s s s triangle. We were given 3 lowercase letters. Those are the three sides of the triangle. Now we're just going to be solving for the 3 angles. We're basically just gonna use the law of cosines to do that. So let's just jump right into our second step. 2nd step, it says that if you were given an s s s triangle, you're just gonna find any angle. It doesn't matter which one you choose to start off with. I'm just gonna go ahead and choose to start off with angle a. Alright? To solve for this, I'm gonna use the law of cosines. All of them are just as easy to use, but I want the cosine of a, so I'm just gonna use the sort of first version of this over here. Alright? So in step 2b, what I'm gonna do is set up my equation. I've got a squared equals b squared and then plus c squared. We already know the pattern here. Minus 2bc times the cosine of a. So remember, I'm solving for this angle over here, so I'm going to have to move everything over to the left side. Now whenever you're solving for angles, instead of just plugging stuff in, I'm gonna show you sort of an equation that always ends up sort of like falling out from this when you're solving for an angle because, it's it's gonna be pretty useful. Alright? So we're gonna subtract the b squared and the c squared from both sides, and you'll end up with a squared minus b squared minus c squared. Right? This equals negative 2bc times the cosine of a. Next, I'm just gonna subtract this or I'm gonna divide out this, 2bc from both sides, which you're gonna end up with is it over here. So in other words, what happens is every time you do this, you're always gonna have these sort of the 3 squareds on the top that are subtracted by each other and then the negative of 2 times the other two variables that were over here. And this is gonna equal your angle. This is gonna be a common thing that happens whenever you're solving for an angle like cosine of a. So now that I have this equation, I can just go ahead and plug in all the numbers here. Just makes things a little bit quicker. Alright? So I've got a squared minus b squared minus c squared. Some of the words, I've got 5 squared minus 15 squared minus 13 squared. That's going to be on the top. And on the bottom, you're gonna have negative 2 times b, which is 15, times b c, which is 13. So if you go ahead and solve for this, what you're gonna see is that this ends up being 0.946. Alright? So if this is 0.946, that means that we figure out a by taking the inverse cosine of this number over here, 0.946. What you'll end up with here when you take the inverse cosine is you're gonna end up with 18.9 degrees, and that makes sense. You also don't have to check for a second angle because this always just gives you one. This totally makes sense because this is the sort of skinniest angle in our triangle. This is the smallest one. And so totally makes sense. This is 18.9 degrees. Alright. One step closer. That's our first angle. Let's move on to the second step over here, which is, basically, we're just gonna continue using the law of cosines to find a second angle. Alright? So we're gonna find the we're gonna use the exact same sort of equation and the same setup, except we're just gonna solve for another angle. Alright? Again, it doesn't matter which one which one you choose. We we only have 2 variables or 2 angles left to solve for, b and c. I'm just gonna go ahead and solve for b. If you chose to do it a different way, totally fine. Alright? So this is step 3. I'm just gonna set up the exact same equation. B squared is equal to a squared plus c squared minus 2ac times the cosine of b. And rather than sort of work this out again, I'm just actually just gonna go ahead and skip to this. Cosine of b, when you work this out, is actually just gonna equal b squared minus a squared minus c squared. That's gonna be on the top. And then the bottom is just gonna be negative 2 a c. Alright. You can pause the video and basically use the exact same steps that we did over here, but you should see that this is what the equation works out to be for cosine of big B. Alright. So this is just going to be what I've got here is, I've got this is going to be 15 squared minus 5 squared minus 13 squared. That's gonna be on the top. And then on the bottom, this is gonna be negative 2 times a, which is the 5 and then times c, which is the 13. When you go ahead and work this out, what you're gonna get is that cosine of b is that cosine of b is equal to this whole mess over here, which turns out to be, negative 0.238. It's always a good idea to hang on to a couple of extra decimal signs. Alright? So if you wanna solve for b, you just have to take the cosine inverse. To take the cone cosine inverse of negative 0.238. So it would be fine. You can take a cosine inverses of negative numbers. So what you're gonna get is you're gonna get something that is greater than 90 degrees. And that's exactly what we get here. We get something that is a 103.8 degrees. Alright. So that is our second angle over here. Notice how if we go back up to the diagram, this totally makes sense because we have that this angle b over here is a is an obtuse angle. It's something that's a little bit more than 90 degrees. This ends up being 103.8. Alright? So last step, how do we solve for this missing angle? Well, you probably guessed that whenever you have 2 angles, you can always solve for the other one using the angle sum formula. Pretty straightforward here. All we're gonna do is I'm actually just gonna do this over here, step 4. We're just gonna say that a plus b plus c is equal to 180 degrees. Only thing left to solve for is c, so you just subtract the other two angles. 180 minus 18.9 minus 103.8. And if you work that out, what you'll end up getting is you'll end up getting 57.3 degrees, and that totally makes sense. Go back to our triangle the way it's drawn over here. This looks to be about a 57.3 degree angle. Alright? So very straightforward with the law of cosines for a triple s triangle, you basically just use the law of sines cosines twice to find 2 angles, and then you can always just find the third one pretty straightforward. Alright? Thanks for watching, and I'll see you in the next one.

Solve the triangle : a = 5 a=5 a = 5 , b = 15 b=15 b = 15 , c = 13 c=13 c = 13 .

A = 18.9 ° , B = 103.8 ° , C = 57.3 ° A=18.9\degree,B=103.8\degree,C=57.3\degree A = 18.9° , B = 103.8° , C = 57.3°

A = 13.8 ° , B = 108.9 ° , C = 57.3 ° A=13.8\degree,B=108.9\degree,C=57.3\degree A = 13.8° , B = 108.9° , C = 57.3°

A = 13.8 ° , B = 103.8 ° , C = 62.4 ° A=13.8\degree,B=103.8\degree,C=62.4\degree A = 13.8° , B = 103.8° , C = 62.4°

A = 18.9 ° , B = 98.7 ° , C = 62.4 ° A=18.9\degree,B=98.7\degree,C=62.4\degree A = 18.9° , B = 98.7° , C = 62.4°

13. Non-Right Triangles

Law of Cosines

Precalculus

13. Non-Right Triangles

Law of Cosines

Struggling with Precalculus?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

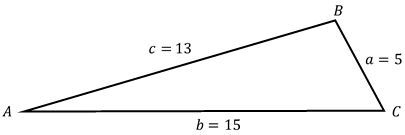
Solve the triangle: $a=5$ , $b=15$ , $c=13$ .

$A=18.9\degree,B=103.8\degree,C=57.3\degree$

$A=13.8\degree,B=108.9\degree,C=57.3\degree$

$A=13.8\degree,B=103.8\degree,C=62.4\degree$

$A=18.9\degree,B=98.7\degree,C=62.4\degree$

Verified step by step guidance

Identify the given sides of the triangle: a = 5, b = 15, c = 13.

Use the Law of Cosines to find one of the angles. For example, to find angle A, use the formula: cos(A) = (b^2 + c^2 - a^2) / (2bc).

Substitute the values into the formula: cos(A) = (15^2 + 13^2 - 5^2) / (2 * 15 * 13).

Calculate the value of cos(A) and then use the inverse cosine function to find angle A.

Repeat the process using the Law of Cosines to find another angle, such as angle B, and then use the fact that the sum of angles in a triangle is 180° to find the third angle, C.

4:35m

Watch next

Master Intro to Law of Cosines with a bite sized video explanation from Patrick

Start learning