In trigonometry, understanding the graphs of the cosecant and secant functions is essential, as they are the reciprocals of the sine and cosine functions, respectively. The cosecant function is defined as \( \csc(x) = \frac{1}{\sin(x)} \) and the secant function as \( \sec(x) = \frac{1}{\cos(x)} \). This relationship allows us to derive their graphs from the sine and cosine graphs.
When graphing the cosecant function, it is important to note that wherever the sine function equals zero, the cosecant will be undefined. This leads to vertical asymptotes at these points. For example, the sine function is zero at \( x = 0, \pi, 2\pi \), which means the cosecant function will have asymptotes at these values. The behavior of the cosecant function can be visualized by taking the reciprocal of the sine values. As the sine values approach zero, the cosecant values approach infinity, resulting in a graph that features "smiley" and "frowny" shapes between the asymptotes.
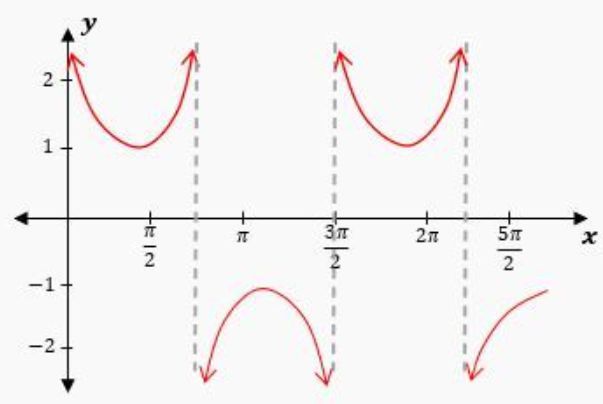
Similarly, for the secant function, the cosine function's zeros indicate where the secant function is undefined, leading to asymptotes at \( x = \frac{\pi}{2}, \frac{3\pi}{2}, \frac{5\pi}{2} \). The secant graph also exhibits similar "smiley" and "frowny" shapes, but the locations of the asymptotes differ from those of the cosecant function.
Transformations applied to sine and cosine functions, such as stretching and shifting, can also be applied to their reciprocal functions. For instance, to graph \( y = \csc(2x) \), one would first graph \( y = \sin(2x) \) to determine the key points and asymptotes. The period of the sine function is calculated using the formula \( \text{Period} = \frac{2\pi}{b} \), where \( b \) is the coefficient of \( x \). In this case, with \( b = 2 \), the period becomes \( \pi \). The sine graph will have peaks and valleys at intervals of \( \frac{\pi}{2} \), and the cosecant graph will have asymptotes at these points, with the corresponding "smiley" and "frowny" shapes filling the spaces between the asymptotes.
In summary, the cosecant and secant functions can be effectively graphed by understanding their relationships to the sine and cosine functions, recognizing where they are undefined, and applying transformation rules. This approach allows for a comprehensive understanding of their behavior and graphical representation.