Using the graph, find the specified limit or state that the limit does not exist (DNE). lim ⁡ x → − 2 − f ( x ) \lim_{x\rarr-2^{-}}f\left(x\right) lim x → − 2 − f ( x ) , lim ⁡ x → − 2 + f ( x ) \lim_{x\rarr-2^{+}}f\left(x\right) lim x → − 2 + f ( x ) , lim ⁡ x → − 2 f ( x ) \lim_{x\rarr-2^{}}f\left(x\right) lim x → − 2 f ( x )

lim ⁡ x → − 2 − f ( x ) = 1 \lim_{x\rarr-2^{-}}f\left(x\right)=1 lim x → − 2 − f ( x ) = 1 , lim ⁡ x → − 2 + f ( x ) = 1 \lim_{x\rarr-2^{+}}f\left(x\right)=1 lim x → − 2 + f ( x ) = 1 , lim ⁡ x → − 2 f ( x ) = 1 \lim_{x\rarr-2^{}}f\left(x\right)=1 lim x → − 2 f ( x ) = 1

lim ⁡ x → − 2 − f ( x ) = 1 \lim_{x\rarr-2^{-}}f\left(x\right)=1 lim x → − 2 − f ( x ) = 1 , lim ⁡ x → − 2 + f ( x ) = − 1 \lim_{x\rarr-2^{+}}f\left(x\right)=-1 lim x → − 2 + f ( x ) = − 1 , lim ⁡ x → − 2 f ( x ) = D N E \lim_{x\rarr-2}f\left(x\right)=DNE lim x → − 2 f ( x ) = D NE

lim ⁡ x → − 2 − f ( x ) = 1 \lim_{x\rarr-2^{-}}f\left(x\right)=1 lim x → − 2 − f ( x ) = 1 , lim ⁡ x → − 2 + f ( x ) = 1 \lim_{x\rarr-2^{+}}f\left(x\right)=1 lim x → − 2 + f ( x ) = 1 , lim ⁡ x → − 2 f ( x ) = D N E \lim_{x\rarr-2}f\left(x\right)=DNE lim x → − 2 f ( x ) = D NE

lim ⁡ x → − 2 − f ( x ) = 0 \lim_{x\rarr-2^{-}}f\left(x\right)=0 lim x → − 2 − f ( x ) = 0 , lim ⁡ x → − 2 + f ( x ) = 0 \lim_{x\rarr-2^{+}}f\left(x\right)=0 lim x → − 2 + f ( x ) = 0 , lim ⁡ x → − 2 f ( x ) = 0 \lim_{x\rarr-2}f\left(x\right)=0 lim x → − 2 f ( x ) = 0

Using the graph, find the specified limit or state that the limit does not exist (DNE). lim ⁡ x → 0 − f ( x ) \lim_{x\rightarrow0^{-}}f\left(x\right) lim x → 0 − f ( x ) , lim ⁡ x → 0 + f ( x ) \lim_{x\rightarrow0^{+}}f\left(x\right) lim x → 0 + f ( x ) , lim ⁡ x → 0 f ( x ) \lim_{x\rightarrow0}f\left(x\right) lim x → 0 f ( x )

lim ⁡ x → 0 − f ( x ) = 0 \lim_{x\rightarrow0^{-}}f\left(x\right)=0 lim x → 0 − f ( x ) = 0 , lim ⁡ x → 0 + f ( x ) = 0 \lim_{x\rightarrow0^{+}}f\left(x\right)=0 lim x → 0 + f ( x ) = 0 , lim ⁡ x → 0 f ( x ) = 0 \lim_{x\rightarrow0}f\left(x\right)=0 lim x → 0 f ( x ) = 0

lim ⁡ x → 0 − f ( x ) = 0 \lim_{x\rightarrow0^{-}}f\left(x\right)=0 lim x → 0 − f ( x ) = 0 , lim ⁡ x → 0 + f ( x ) = 0 \lim_{x\rightarrow0^{+}}f\left(x\right)=0 lim x → 0 + f ( x ) = 0 , lim ⁡ x → 0 f ( x ) = D N E \lim_{x\rightarrow0}f\left(x\right)=DNE lim x → 0 f ( x ) = D NE

lim ⁡ x → 0 − f ( x ) = − 1 \lim_{x\rightarrow0^{-}}f\left(x\right)=-1 lim x → 0 − f ( x ) = − 1 , lim ⁡ x → 0 + f ( x ) = − 1 \lim_{x\rightarrow0^{+}}f\left(x\right)=-1 lim x → 0 + f ( x ) = − 1 , lim ⁡ x → 0 f ( x ) = D N E \lim_{x\rightarrow0}f\left(x\right)=DNE lim x → 0 f ( x ) = D NE

lim ⁡ x → 0 − f ( x ) = − 1 \lim_{x\rightarrow0^{-}}f\left(x\right)=-1 lim x → 0 − f ( x ) = − 1 , lim ⁡ x → 0 + f ( x ) = − 1 \lim_{x\rightarrow0^{+}}f\left(x\right)=-1 lim x → 0 + f ( x ) = − 1 , lim ⁡ x → 0 f ( x ) = − 1 \lim_{x\rightarrow0}f\left(x\right)=-1 lim x → 0 f ( x ) = − 1

Using the graph, find the specified limit or state that the limit does not exist. lim ⁡ x → 4 − f ( x ) \lim_{x\rightarrow4^{-}}f\left(x\right) lim x → 4 − f ( x ) , lim ⁡ x → 4 + f ( x ) \lim_{x\rightarrow4^{+}}f\left(x\right) lim x → 4 + f ( x ) , lim ⁡ x → 4 f ( x ) \lim_{x\rightarrow4}f\left(x\right) lim x → 4 f ( x )

lim ⁡ x → 4 − f ( x ) = 1 \lim_{x\rightarrow4^{-}}f\left(x\right)=1 lim x → 4 − f ( x ) = 1 , lim ⁡ x → 4 + f ( x ) = 3 \lim_{x\rightarrow4^{+}}f\left(x\right)=3 lim x → 4 + f ( x ) = 3 , lim ⁡ x → 4 f ( x ) = D N E \lim_{x\rightarrow4}f\left(x\right)=DNE lim x → 4 f ( x ) = D NE

lim ⁡ x → 4 − f ( x ) = 1 \lim_{x\rightarrow4^{-}}f\left(x\right)=1 lim x → 4 − f ( x ) = 1 , lim ⁡ x → 4 + f ( x ) = 1 \lim_{x\rightarrow4^{+}}f\left(x\right)=1 lim x → 4 + f ( x ) = 1 , lim ⁡ x → 4 f ( x ) = 1 \lim_{x\rightarrow4}f\left(x\right)=1 lim x → 4 f ( x ) = 1

lim ⁡ x → 4 − f ( x ) = 3 \lim_{x\rightarrow4^{-}}f\left(x\right)=3 lim x → 4 − f ( x ) = 3 , lim ⁡ x → 4 + f ( x ) = 3 \lim_{x\rightarrow4^{+}}f\left(x\right)=3 lim x → 4 + f ( x ) = 3 , lim ⁡ x → 4 f ( x ) = 3 \lim_{x\rightarrow4}f\left(x\right)=3 lim x → 4 f ( x ) = 3

lim ⁡ x → 4 − f ( x ) = 3 \lim_{x\rightarrow4^{-}}f\left(x\right)=3 lim x → 4 − f ( x ) = 3 , lim ⁡ x → 4 + f ( x ) = 1 \lim_{x\rightarrow4^{+}}f\left(x\right)=1 lim x → 4 + f ( x ) = 1 , lim ⁡ x → 4 f ( x ) = D N E \lim_{x\rightarrow4}f\left(x\right)=DNE lim x → 4 f ( x ) = D NE

Find the specified limit or state that the limit does not exist by creating a table of values. f ( x ) = 1 x f\left(x\right)=\frac{1}{x} f ( x ) = x 1 lim ⁡ x → 1 − f ( x ) \lim_{x\rightarrow1^{-}}f\left(x\right) lim x → 1 − f ( x ) , lim ⁡ x → 1 + f ( x ) \lim_{x\rightarrow1^{+}}f\left(x\right) lim x → 1 + f ( x ) , lim ⁡ x → 1 f ( x ) \lim_{x\rightarrow1}f\left(x\right) lim x → 1 f ( x )

lim ⁡ x → 1 − f ( x ) = 1 \lim_{x\rightarrow1^{-}}f\left(x\right)=1 lim x → 1 − f ( x ) = 1 , lim ⁡ x → 1 + f ( x ) = 1 \lim_{x\rightarrow1^{+}}f\left(x\right)=1 lim x → 1 + f ( x ) = 1 , lim ⁡ x → 1 f ( x ) = 1 \lim_{x\rightarrow1}f\left(x\right)=1 lim x → 1 f ( x ) = 1

lim ⁡ x → 1 − f ( x ) = 0 \lim_{x\rightarrow1^{-}}f\left(x\right)=0 lim x → 1 − f ( x ) = 0 , lim ⁡ x → 1 + f ( x ) = 0 \lim_{x\rightarrow1^{+}}f\left(x\right)=0 lim x → 1 + f ( x ) = 0 , lim ⁡ x → 1 f ( x ) = 1 \lim_{x\rightarrow1}f\left(x\right)=1 lim x → 1 f ( x ) = 1

lim ⁡ x → 1 − f ( x ) = 1 \lim_{x\rightarrow1^{-}}f\left(x\right)=1 lim x → 1 − f ( x ) = 1 , lim ⁡ x → 1 + f ( x ) = − 1 \lim_{x\rightarrow1^{+}}f\left(x\right)=-1 lim x → 1 + f ( x ) = − 1 , lim ⁡ x → 1 f ( x ) = D N E \lim_{x\rightarrow1}f\left(x\right)=DNE lim x → 1 f ( x ) = D NE

lim ⁡ x → 1 − f ( x ) = − 1 \lim_{x\rightarrow1^{-}}f\left(x\right)=-1 lim x → 1 − f ( x ) = − 1 , lim ⁡ x → 1 + f ( x ) = − 1 \lim_{x\rightarrow1^{+}}f\left(x\right)=-1 lim x → 1 + f ( x ) = − 1 , lim ⁡ x → 1 f ( x ) = − 1 \lim_{x\rightarrow1}f\left(x\right)=-1 lim x → 1 f ( x ) = − 1

22. Limits & Continuity

Introduction to Limits

22. Limits & Continuity

Introduction to Limits: Videos & Practice Problems

Video Lessons Practice Worksheet

Topic summary

Limits are fundamental in calculus, representing the y-value a function approaches as x nears a specific value from either side. This can be analyzed graphically or numerically. One-sided limits, denoted with negative or positive signs, help determine if a limit exists. If the left and right limits differ, the limit does not exist (DNE). Additionally, limits can fail to exist due to unbounded behavior or oscillation near a point. Understanding these concepts is crucial for analyzing functions and their behaviors in calculus.

concept

Finding Limits Numerically and Graphically

Video duration:

Finding Limits Numerically and Graphically Video Summary

Limits are fundamental concepts in calculus that help us understand the behavior of functions as they approach a specific value. When we talk about limits, we are interested in what a function is doing around a certain value of x, rather than at that exact point. This can be visualized through graphs or analyzed using tables of values.

The notation for limits is typically expressed as $\lim_{{x \to c}} f(x)$, which reads as "the limit of f of x as x approaches c." For example, to find the limit of the function $f(x) = x^2$ as $x$ approaches 2, we examine the y-values that $f(x)$ approaches as $x$ gets very close to 2. This means we consider values like 1.99 and 2.01, which yield results of 3.96 and 4.04, respectively. Both sides approach a y-value of 4, leading us to conclude that $\lim_{{x \to 2}} x^2 = 4$.

Another example involves the function $f(x) = x + 4$ as $x$ approaches 1. By evaluating values close to 1, such as 0.99 and 1.01, we find that both sides approach a y-value of 5. Thus, $\lim_{{x \to 1}} (x + 4) = 5$. It's important to note that while plugging in the value of c directly into the function can yield the limit, this is not always reliable. There are cases where the limit does not equal the function value at that point.

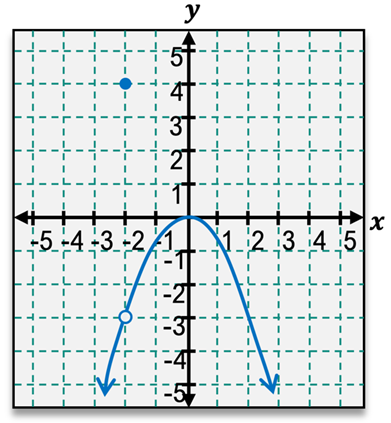
For instance, when examining a different function as $x$ approaches 3, we may find that the limit is 1 based on the graph, even if the function value at $x = 3$ is 4. This discrepancy highlights the necessity of focusing on the behavior of the function around the point rather than the value at the point itself. Therefore, understanding limits requires careful analysis of the function's approach to a given value, ensuring we capture the correct behavior of the function.

Problem

Find the limit by creating a table of values.
$\lim_{x\rarr0}-4x+2$

$-4$

$-2$

$0$

$2$

Problem

Find the limit by creating a table of values.
$\lim_{x\rarr2}3x^2+5x+1$

$1$

$10$

$23$

$21$

Problem

Find the limit by creating a table of values.
$\lim_{x\rarr1}\frac{x^2-4}{x-2}$

$0$

$3$

$-3$

$2$

Problem

Find the limit using the graph of $f\left(x\right)$ shown.
$\lim_{x\rarr1}f\left(x\right)$

$2$

$1$

$0$

Unable to determine

Problem

Find the limit using the graph of $f\left(x\right)$ shown.
$\lim_{x\rarr-2}f\left(x\right)$

$4$

$-2$

$-3$

Unable to determine

Problem

Find the limit using the graph of $f\left(x\right)$ shown.
$\lim_{x\rarr4}f\left(x\right)$

$2$

$-2$

$0$

Unable to determine

example

Finding Limits Numerically and Graphically Example 1

Video duration:

Finding Limits Numerically and Graphically Example 1 Video Summary

In analyzing limits using a graph, it's essential to observe the behavior of the function as the input approaches a specific value from both the left and right sides. For instance, when determining the limit of $ f(x) $ as $ x $ approaches $-2$, we find that the function approaches a value of $ 1 $ from both directions. Therefore, we conclude that:

\[ \lim_{{x \to -2}} f(x) = 1 \]

Next, we examine the limit of $ f(x) $ as $ x $ approaches $ 0 $. Despite a hole in the graph at this point, the function approaches $ 0 $ from both sides. This reinforces the concept that the limit focuses on the behavior near the point rather than the actual value at that point. Thus, we have:

\[ \lim_{{x \to 0}} f(x) = 0 \]

Finally, when considering the limit of $ f(x) $ as $ x $ approaches $ 3 $, the function again approaches $ 1 $ from both sides, leading to the conclusion:

\[ \lim_{{x \to 3}} f(x) = 1 \]

However, as we approach $ x = 4 $, we encounter a situation where the left-hand limit and right-hand limit do not match. This discrepancy indicates that the limit does not exist at that point, highlighting the importance of checking both sides when evaluating limits. Understanding these concepts is crucial for mastering the behavior of functions and their limits in calculus.

concept

One-Sided Limits

Video duration:

One-Sided Limits Video Summary

When determining the limit of a function as $ x $ approaches a specific value, we focus on the $ y $ value that the function approaches from either side of that value. This process involves evaluating one-sided limits, which are expressed using specific notation. The left-sided limit is denoted as $ \lim_{{x \to c^-}} f(x) $, indicating that $ x $ approaches $ c $ from the left, while the right-sided limit is represented as $ \lim_{{x \to c^+}} f(x) $, showing that $ x $ approaches $ c $ from the right. A helpful way to remember this is that $ x $ values from the left are negative, and those from the right are positive.

To illustrate, consider a piecewise function where we want to find the left-sided limit as $ x $ approaches 3. By examining the graph or substituting values slightly less than 3 (like 2.99 and 2.999), we find that the function approaches a $ y $ value of 1. Thus, we conclude that $ \lim_{{x \to 3^-}} f(x) = 1 $.

Next, for the right-sided limit as $ x $ approaches 3, we look at values slightly greater than 3 (like 3.01 and 3.001). Here, the function approaches a $ y $ value of 4, leading to $ \lim_{{x \to 3^+}} f(x) = 4 $.

When we evaluate the overall limit $ \lim_{{x \to 3}} f(x) $, we notice that the left-sided limit (1) and the right-sided limit (4) are not equal. This discrepancy indicates that the limit does not exist, often abbreviated as DNE (Does Not Exist).

In another example, we can find the left-sided limit as $ x $ approaches 1, which yields $ \lim_{{x \to 1^-}} f(x) = -1 $. For the right-sided limit, we find $ \lim_{{x \to 1^+}} f(x) = -1 $ as well. Since both one-sided limits are equal, we conclude that the overall limit $ \lim_{{x \to 1}} f(x) = -1 $ exists.

In summary, when working with one-sided limits, if the left-sided and right-sided limits are not the same, the overall limit does not exist. Conversely, if they are equal, the overall limit exists and is equal to that common value. This understanding is crucial for analyzing the behavior of functions at specific points.

Problem

Using the graph, find the specified limit or state that the limit does not exist (DNE).
$\lim_{x\rarr-2^{-}}f\left(x\right)$ , $\lim_{x\rarr-2^{+}}f\left(x\right)$ , $\lim_{x\rarr-2^{}}f\left(x\right)$

$\lim_{x\rarr-2^{-}}f\left(x\right)=1$ , $\lim_{x\rarr-2^{+}}f\left(x\right)=1$ , $\lim_{x\rarr-2^{}}f\left(x\right)=1$

$\lim_{x\rarr-2^{-}}f\left(x\right)=1$ , $\lim_{x\rarr-2^{+}}f\left(x\right)=-1$ , $\lim_{x\rarr-2}f\left(x\right)=DNE$

$\lim_{x\rarr-2^{-}}f\left(x\right)=1$ , $\lim_{x\rarr-2^{+}}f\left(x\right)=1$ , $\lim_{x\rarr-2}f\left(x\right)=DNE$

$\lim_{x\rarr-2^{-}}f\left(x\right)=0$ , $\lim_{x\rarr-2^{+}}f\left(x\right)=0$ , $\lim_{x\rarr-2}f\left(x\right)=0$

Problem

Using the graph, find the specified limit or state that the limit does not exist (DNE).
$\lim_{x\rightarrow0^{-}}f\left(x\right)$ , $\lim_{x\rightarrow0^{+}}f\left(x\right)$ , $\lim_{x\rightarrow0}f\left(x\right)$

$\lim_{x\rightarrow0^{-}}f\left(x\right)=0$ , $\lim_{x\rightarrow0^{+}}f\left(x\right)=0$ , $\lim_{x\rightarrow0}f\left(x\right)=0$

$\lim_{x\rightarrow0^{-}}f\left(x\right)=0$ , $\lim_{x\rightarrow0^{+}}f\left(x\right)=0$ , $\lim_{x\rightarrow0}f\left(x\right)=DNE$

$\lim_{x\rightarrow0^{-}}f\left(x\right)=-1$ , $\lim_{x\rightarrow0^{+}}f\left(x\right)=-1$ , $\lim_{x\rightarrow0}f\left(x\right)=DNE$

$\lim_{x\rightarrow0^{-}}f\left(x\right)=-1$ , $\lim_{x\rightarrow0^{+}}f\left(x\right)=-1$ , $\lim_{x\rightarrow0}f\left(x\right)=-1$

Problem

Using the graph, find the specified limit or state that the limit does not exist.
$\lim_{x\rightarrow4^{-}}f\left(x\right)$ , $\lim_{x\rightarrow4^{+}}f\left(x\right)$ , $\lim_{x\rightarrow4}f\left(x\right)$

$\lim_{x\rightarrow4^{-}}f\left(x\right)=1$ , $\lim_{x\rightarrow4^{+}}f\left(x\right)=1$ , $\lim_{x\rightarrow4}f\left(x\right)=1$

$\lim_{x\rightarrow4^{-}}f\left(x\right)=3$ , $\lim_{x\rightarrow4^{+}}f\left(x\right)=3$ , $\lim_{x\rightarrow4}f\left(x\right)=3$

$\lim_{x\rightarrow4^{-}}f\left(x\right)=3$ , $\lim_{x\rightarrow4^{+}}f\left(x\right)=1$ , $\lim_{x\rightarrow4}f\left(x\right)=DNE$

$\lim_{x\rightarrow4^{-}}f\left(x\right)=1$ , $\lim_{x\rightarrow4^{+}}f\left(x\right)=3$ , $\lim_{x\rightarrow4}f\left(x\right)=DNE$

Problem

Find the specified limit or state that the limit does not exist by creating a table of values.
$f\left(x\right)=\frac{1}{x}$
$\lim_{x\rightarrow1^{-}}f\left(x\right)$ , $\lim_{x\rightarrow1^{+}}f\left(x\right)$ , $\lim_{x\rightarrow1}f\left(x\right)$

$\lim_{x\rightarrow1^{-}}f\left(x\right)=0$ , $\lim_{x\rightarrow1^{+}}f\left(x\right)=0$ , $\lim_{x\rightarrow1}f\left(x\right)=1$

$\lim_{x\rightarrow1^{-}}f\left(x\right)=1$ , $\lim_{x\rightarrow1^{+}}f\left(x\right)=1$ , $\lim_{x\rightarrow1}f\left(x\right)=1$

$\lim_{x\rightarrow1^{-}}f\left(x\right)=1$ , $\lim_{x\rightarrow1^{+}}f\left(x\right)=-1$ , $\lim_{x\rightarrow1}f\left(x\right)=DNE$

$\lim_{x\rightarrow1^{-}}f\left(x\right)=-1$ , $\lim_{x\rightarrow1^{+}}f\left(x\right)=-1$ , $\lim_{x\rightarrow1}f\left(x\right)=-1$

concept

Cases Where Limits Do Not Exist

Video duration:

Cases Where Limits Do Not Exist Video Summary

Understanding when a limit does not exist is crucial in calculus, as it helps in analyzing the behavior of functions. There are several scenarios where limits fail to exist, and recognizing these can enhance your problem-solving skills.

One common case occurs with piecewise functions that exhibit a jump discontinuity. For instance, consider the limit of a function $ f(x) $ as $ x $ approaches 3. If the function approaches a value of 1 from the left and a value of 4 from the right, the limit does not exist because the left-hand limit and right-hand limit are not equal. This discontinuity indicates that the function jumps from one value to another, which is a typical characteristic of piecewise functions.

Another scenario involves unbounded behavior, particularly with rational functions that have vertical asymptotes. For example, if we examine the limit of $ f(x) $ as $ x $ approaches 2 and find that the function approaches infinity from both sides, we conclude that the limit does not exist. This is because infinity is not a finite number, and thus, we cannot assign a limit in this case. It’s important to note that while we may describe the behavior of the function as approaching positive or negative infinity, this does not imply the existence of a limit.

Lastly, limits can also fail to exist due to oscillation. For instance, if we look at the limit of $ f(x) $ as $ x $ approaches 0 and observe that the function oscillates wildly, such as in the case of $ \sin(1/x) $ or $ \cos(1/x) $, the limit does not exist. Even if we zoom in on the graph, the oscillation persists, preventing us from determining a single value that the function approaches.

In summary, limits do not exist in cases of jump discontinuities, unbounded behavior, and oscillation. Recognizing these patterns will aid in your understanding of limits and their applications in calculus.

example

Cases Where Limits Do Not Exist Example 2

Video duration:

Cases Where Limits Do Not Exist Example 2 Video Summary

Understanding limits is crucial in calculus, particularly when analyzing the behavior of functions as they approach specific values. In this context, we will explore how to estimate limits using graphical representations and identify when limits do not exist.

To begin, consider the limit of $ f(x) $ as $ x $ approaches $-2$. By examining the graph, we observe that as $ x $ approaches $-2$ from the left, $ f(x) $ approaches $ 0 $. Similarly, as $ x $ approaches $-2$ from the right, $ f(x) $ also approaches $ 0 $. Therefore, we conclude that:

\[ \lim_{{x \to -2}} f(x) = 0 \]

It is important to note that the behavior of the function at values other than $-2$ does not affect the limit, as we are only concerned with values infinitesimally close to $-2$.

Next, we analyze the limit of $ f(x) $ as $ x $ approaches $ 0 $. From the graph, as $ x $ approaches $ 0 $ from the left, $ f(x) $ approaches $ 1 $, and from the right, it also approaches $ 1 $. Thus, we find that:

\[ \lim_{{x \to 0}} f(x) = 1 \]

Even though there is a hole in the graph at $ x = 0 $ where $ f(0) = -2 $, this does not impact the limit since we are focused on the values approaching $ 0 $.

Finally, we examine the limit of $ f(x) $ as $ x $ approaches $-3$. Observing the graph, as $ x $ approaches $-3$ from the left, $ f(x) $ approaches $ 1 $. However, from the right, $ f(x) $ exhibits unbounded behavior, tending towards negative infinity. This discrepancy indicates that the one-sided limits are not equal:

\[ \lim_{{x \to -3^-}} f(x) = 1 \quad \text{and} \quad \lim_{{x \to -3^+}} f(x) = -\infty \]

Since the left-hand limit and the right-hand limit do not match, we conclude that:

\[ \lim_{{x \to -3}} f(x) \text{ does not exist} \]

In summary, when evaluating limits, it is essential to consider the behavior of the function as it approaches the specified value from both sides. Discrepancies in one-sided limits or unbounded behavior indicate that the overall limit does not exist.

Problem

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).
$\lim_{x\rarr1}f\left(x\right)$

$0$

$1$

$2$

DNE

Problem

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).
$\lim_{x\rarr-2}f\left(x\right)$

$-3$

$1$

$4$

DNE

Problem

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).
$\lim_{x\rarr0}f\left(x\right)$

$0$

$1$

$5$

DNE

Problem

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).
$lim over x right arrow 0 of f of x$

$-1$

$0$

$1$

DNE

Do you want more practice?

We have more practice problems on Introduction to Limits

Go over this topic definitions with flashcards

More sets

Introduction to Limits definitions
22. Limits & Continuity
15 Terms

Here’s what students ask on this topic:

What is the definition of a limit in calculus?

A limit in calculus is the value that a function (f(x)) approaches as the input (x) approaches a certain value (c). Formally, the limit of f(x) as x approaches c is denoted as:

$lim x_{\to c} f (x)$

This means that as x gets arbitrarily close to c from either side, the function f(x) gets arbitrarily close to a specific value L. Limits are fundamental in understanding the behavior of functions at specific points, especially where the function may not be explicitly defined.

How do you find the limit of a function using a graph?

To find the limit of a function using a graph, follow these steps:

Identify the point c at which you want to find the limit.
Observe the behavior of the function as x approaches c from the left (x → c^-) and from the right (x → c⁺).
If the function approaches the same y-value from both sides, that y-value is the limit.
If the function approaches different y-values from each side, the limit does not exist (DNE).

For example, if you want to find the limit of f(x) as x approaches 2, look at the y-values the function approaches as x gets close to 2 from both sides. If both sides approach the same y-value, that is your limit.

What are one-sided limits and how are they different from regular limits?

One-sided limits consider the behavior of a function as x approaches a specific value from only one side—either from the left or the right. They are denoted as:

Left-sided limit: $lim x_{\to c -} f (x)$

Right-sided limit: $lim x_{\to c +} f (x)$

Regular limits require that the function approaches the same value from both sides. If the left-sided and right-sided limits are equal, the regular limit exists and is equal to that value. If they differ, the regular limit does not exist (DNE).

What are the scenarios in which a limit does not exist?

A limit does not exist (DNE) in the following scenarios:

Different One-Sided Limits: If the left-sided limit and right-sided limit as x approaches c are not equal.
Unbounded Behavior: If the function approaches infinity or negative infinity as x approaches c. For example, rational functions with vertical asymptotes.
Oscillating Behavior: If the function oscillates between values as x approaches c, such as $\sin (\frac{1}{x})$ or $\cos (\frac{1}{x})$ .

In these cases, the function does not approach a single finite value as x approaches c, so the limit does not exist.

How do you find the limit of a function using a table of values?

To find the limit of a function using a table of values, follow these steps:

Choose values of x that get increasingly close to the point c from both the left and the right.
Calculate the corresponding f(x) values for these x values.
Observe the trend of the f(x) values as x approaches c.
If the f(x) values approach the same number from both sides, that number is the limit.

For example, to find the limit of f(x) as x approaches 2, you might use x values like 1.9, 1.99, 1.999 (from the left) and 2.1, 2.01, 2.001 (from the right). If the f(x) values approach the same number, that is your limit.

Your Precalculus tutors

Patrick Ford

Physics and Math Lead Instructor

Introduction to Limits: Videos & Practice Problems

Finding Limits Numerically and Graphically

Finding Limits Numerically and Graphically Video Summary

Find the limit by creating a table of values.limx→0−4x+2\lim_{x\rarr0}-4x+2limx→0−4x+2

Find the limit by creating a table of values.limx→23x2+5x+1\lim_{x\rarr2}3x^2+5x+1limx→23x2+5x+1

Find the limit by creating a table of values.limx→1x2−4x−2\lim_{x\rarr1}\frac{x^2-4}{x-2}limx→1x−2x2−4

Find the limit using the graph of f(x)f\left(x\right)f(x)shown.limx→1f(x)\lim_{x\rarr1}f\left(x\right)limx→1f(x)

Find the limit using the graph of f(x)f\left(x\right)f(x)shown.limx→−2f(x)\lim_{x\rarr-2}f\left(x\right)limx→−2f(x)

Find the limit using the graph of f(x)f\left(x\right)f(x)shown.limx→4f(x)\lim_{x\rarr4}f\left(x\right)limx→4f(x)

Finding Limits Numerically and Graphically Example 1

Finding Limits Numerically and Graphically Example 1 Video Summary

One-Sided Limits

One-Sided Limits Video Summary

Using the graph, find the specified limit or state that the limit does not exist (DNE).limx→−2−f(x)\lim_{x\rarr-2^{-}}f\left(x\right)limx→−2−f(x), limx→−2+f(x)\lim_{x\rarr-2^{+}}f\left(x\right)limx→−2+f(x), limx→−2f(x)\lim_{x\rarr-2^{}}f\left(x\right)limx→−2f(x)

Using the graph, find the specified limit or state that the limit does not exist (DNE).limx→0−f(x)\lim_{x\rightarrow0^{-}}f\left(x\right)limx→0−f(x) , limx→0+f(x)\lim_{x\rightarrow0^{+}}f\left(x\right)limx→0+f(x), limx→0f(x)\lim_{x\rightarrow0}f\left(x\right)limx→0f(x)

Using the graph, find the specified limit or state that the limit does not exist.limx→4−f(x)\lim_{x\rightarrow4^{-}}f\left(x\right)limx→4−f(x), limx→4+f(x)\lim_{x\rightarrow4^{+}}f\left(x\right)limx→4+f(x), limx→4f(x)\lim_{x\rightarrow4}f\left(x\right)limx→4f(x)

Cases Where Limits Do Not Exist

Cases Where Limits Do Not Exist Video Summary

Cases Where Limits Do Not Exist Example 2

Cases Where Limits Do Not Exist Example 2 Video Summary

Use the graph of f(x)f\left(x\right)f(x)to estimate the value of the limit or state that it does not exist (DNE).limx→1f(x)\lim_{x\rarr1}f\left(x\right)limx→1f(x)

Use the graph of f(x)f\left(x\right)f(x)to estimate the value of the limit or state that it does not exist (DNE).limx→−2f(x)\lim_{x\rarr-2}f\left(x\right)limx→−2f(x)

Use the graph of f(x)f\left(x\right)f(x)to estimate the value of the limit or state that it does not exist (DNE).limx→0f(x)\lim_{x\rarr0}f\left(x\right)limx→0f(x)

Use the graph of f(x)f\left(x\right)f(x)to estimate the value of the limit or state that it does not exist (DNE).limx→0f(x)\lim_{x\rarr0}f\left(x\right)

Do you want more practice?

Go over this topic definitions with flashcards

Here’s what students ask on this topic:

What is the definition of a limit in calculus?

How do you find the limit of a function using a graph?

What are one-sided limits and how are they different from regular limits?

What are the scenarios in which a limit does not exist?

How do you find the limit of a function using a table of values?

Your Precalculus tutors

Find the limit by creating a table of values.
$\lim_{x\rarr0}-4x+2$

Find the limit by creating a table of values.
$\lim_{x\rarr2}3x^2+5x+1$

Find the limit by creating a table of values.
$\lim_{x\rarr1}\frac{x^2-4}{x-2}$

Find the limit using the graph of $f\left(x\right)$ shown.
$\lim_{x\rarr1}f\left(x\right)$

Find the limit using the graph of $f\left(x\right)$ shown.
$\lim_{x\rarr-2}f\left(x\right)$

Find the limit using the graph of $f\left(x\right)$ shown.
$\lim_{x\rarr4}f\left(x\right)$

Using the graph, find the specified limit or state that the limit does not exist (DNE).
$\lim_{x\rarr-2^{-}}f\left(x\right)$ , $\lim_{x\rarr-2^{+}}f\left(x\right)$ , $\lim_{x\rarr-2^{}}f\left(x\right)$

Using the graph, find the specified limit or state that the limit does not exist (DNE).
$\lim_{x\rightarrow0^{-}}f\left(x\right)$ , $\lim_{x\rightarrow0^{+}}f\left(x\right)$ , $\lim_{x\rightarrow0}f\left(x\right)$

Using the graph, find the specified limit or state that the limit does not exist.
$\lim_{x\rightarrow4^{-}}f\left(x\right)$ , $\lim_{x\rightarrow4^{+}}f\left(x\right)$ , $\lim_{x\rightarrow4}f\left(x\right)$

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).
$\lim_{x\rarr1}f\left(x\right)$

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).
$\lim_{x\rarr-2}f\left(x\right)$

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).
$\lim_{x\rarr0}f\left(x\right)$

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).
$lim over x right arrow 0 of f of x$