In exploring the graph of the tangent function, it's essential to understand its relationship with sine and cosine. The tangent of an angle can be expressed as the ratio of sine to cosine, represented mathematically as:
\[ \tan(x) = \frac{\sin(x)}{\cos(x)} \]
Starting from the origin, when \( x = 0 \), the tangent value is:
\[ \tan(0) = \frac{\sin(0)}{\cos(0)} = \frac{0}{1} = 0 \]
As we move to \( x = \frac{\pi}{4} \), we find:
\[ \tan\left(\frac{\pi}{4}\right) = \frac{\sin\left(\frac{\pi}{4}\right)}{\cos\left(\frac{\pi}{4}\right)} = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1 \]
Conversely, at \( x = -\frac{\pi}{4} \), the tangent value is:
\[ \tan\left(-\frac{\pi}{4}\right) = \frac{\sin\left(-\frac{\pi}{4}\right)}{\cos\left(-\frac{\pi}{4}\right)} = \frac{-\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = -1 \]
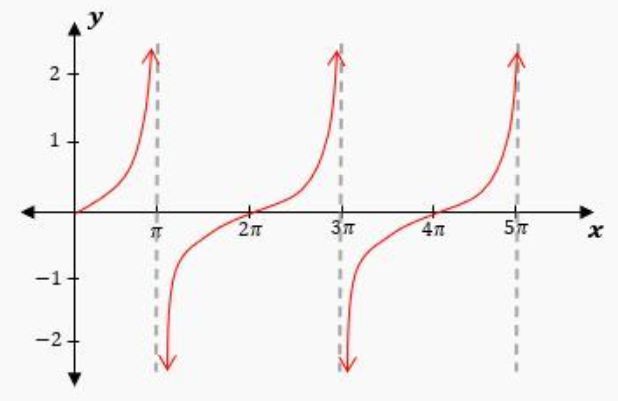
At \( x = \frac{\pi}{2} \) and \( x = -\frac{\pi}{2} \), the tangent function becomes undefined because the cosine value is zero, leading to vertical asymptotes at these points. The graph of the tangent function thus approaches infinity at these asymptotes, which occur at odd multiples of \( \frac{\pi}{2} \), specifically at:
\[ x = \frac{\pi}{2}, \, -\frac{\pi}{2}, \, \frac{3\pi}{2}, \, -\frac{3\pi}{2} \]
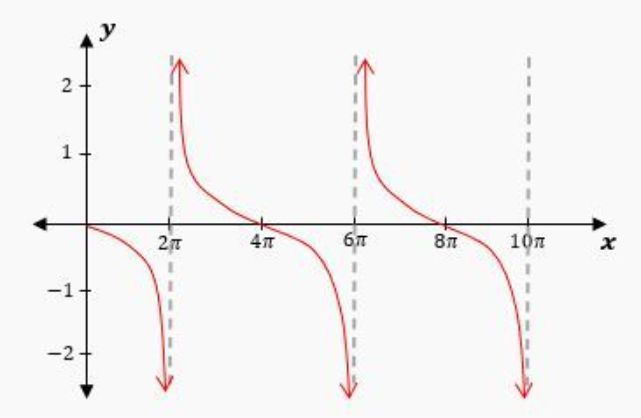
Unlike the secant function, which has a period of \( 2\pi \), the tangent function has a period of \( \pi \). This means the graph repeats every \( \pi \) units along the x-axis. The period can be calculated using the formula:
\[ \text{Period} = \frac{\pi}{b} \]
For example, if we consider the function \( y = \tan\left(\frac{\pi}{2} x\right) \), the coefficient \( b \) is \( \frac{\pi}{2} \). Thus, the period is:
\[ \text{Period} = \frac{\pi}{\frac{\pi}{2}} = 2 \]
This indicates that the tangent function will repeat its pattern every 2 units. To graph this function, we can place asymptotes at \( x = -1 \) and \( x = 1 \), and then extend the graph to the left and right, repeating the curve between these asymptotes. The resulting graph will show the characteristic shape of the tangent function, curving upwards to the right and downwards to the left of each asymptote.
Understanding these properties of the tangent function, including its asymptotes and periodicity, is crucial for accurately graphing and analyzing its behavior in various mathematical contexts.