When exploring polar equations, four primary shapes frequently arise: the cardioid, limacon, rose, and lemniscate. Each of these shapes is characterized by specific equations that include variables such as r, θ, and trigonometric functions.
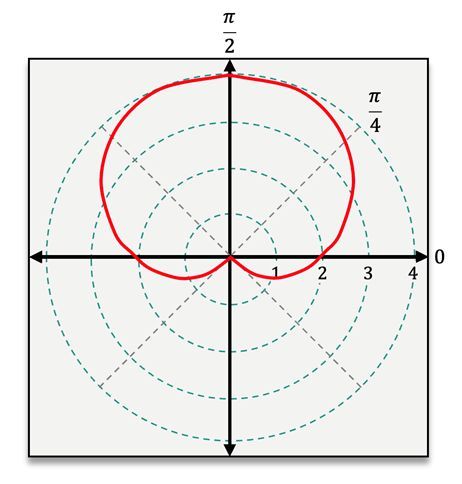
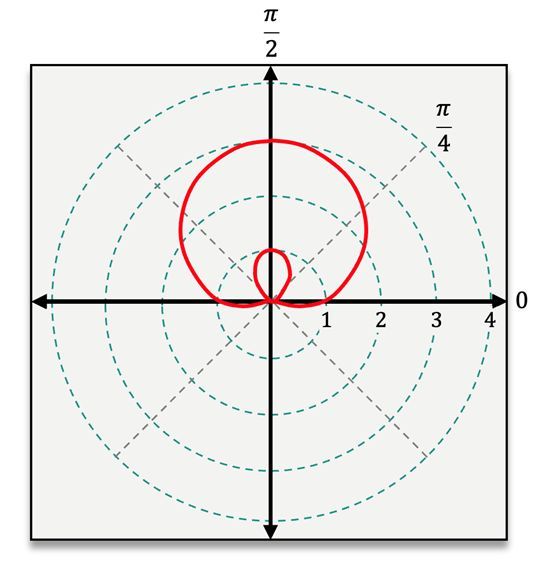
The cardioid resembles a heart shape and is defined by the equations r = a ± b cos(θ) or r = a ± b sin(θ), where both a and b are positive and equal (i.e., a = b). In contrast, the limacon shares the same equation form but allows for a to be either greater than or less than b. If a > b, the limacon has a dimple; if a < b, it features an inner loop. Notably, these equations are the only ones in this context that involve addition or subtraction.
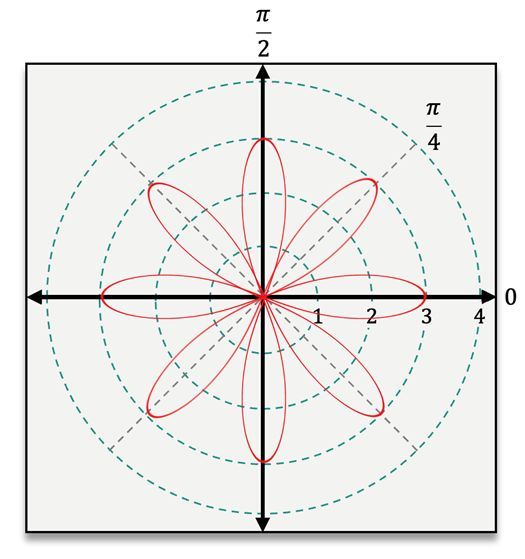
The rose curve, which resembles a flower, is represented by the equations r = a cos(nθ) or r = a sin(nθ). Here, a must be non-zero, and n is an integer greater than or equal to 2, determining the number of petals on the rose. For example, if n = 2, the rose will have two petals.
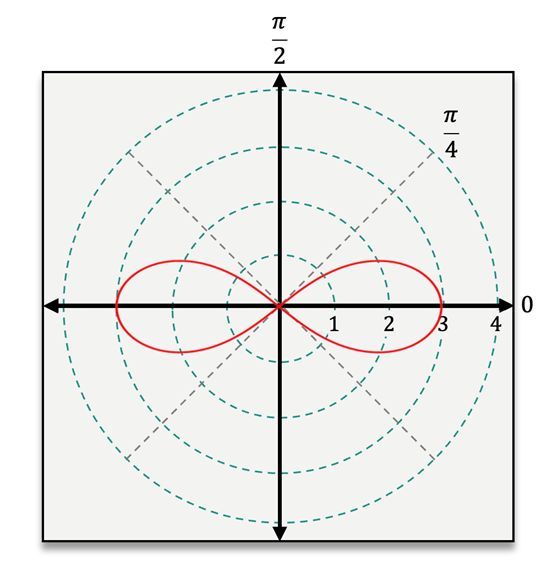
Lastly, the lemniscate, which looks like an infinity symbol, is defined by the equations r² = ±a² cos(2θ) or r² = ±a² sin(2θ). In this case, a cannot be zero, and the presence of r² is a distinctive feature that helps identify this shape.
To classify these equations, consider the following examples: For the equation r = 1 + cos(θ), the addition indicates it could be a cardioid or limacon. Since both a and b are equal to 1, this equation represents a cardioid. In another example, r = 4 sin(2θ), the presence of 2θ suggests a lemniscate, but since it lacks the r² term, it is classified as a rose with n = 2.
Understanding these classifications allows for accurate graphing of polar equations, enhancing comprehension of their geometric representations.