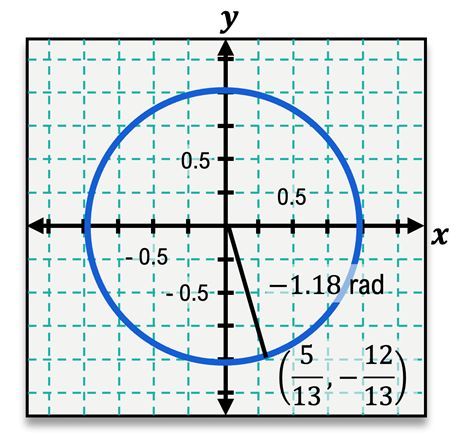
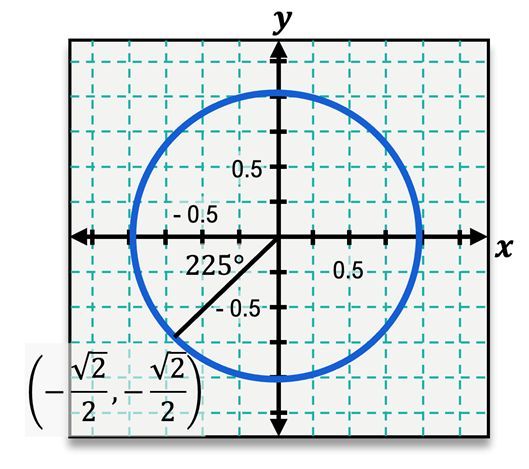
The unit circle is a fundamental concept in trigonometry, where every angle corresponds to a specific point defined by coordinates (x, y) on the circle. The relationship between angles and these coordinates is established through trigonometric functions: sine, cosine, and tangent. These functions can be understood in the context of right triangles formed by the radius of the unit circle, which has a length of 1.
For any angle θ, the sine function is defined as the y-coordinate of the corresponding point on the unit circle, while the cosine function is defined as the x-coordinate. This means that for an angle of 53 degrees, if the coordinates are (3/5, 4/5), then:
\[\sin(53^\circ) = \frac{4}{5}\]
\[\cos(53^\circ) = \frac{3}{5}\]
To remember this relationship, one can note that cosine (c) comes before sine (s) alphabetically, which corresponds to the x-coordinate being the cosine value and the y-coordinate being the sine value.
For the tangent function, it is calculated as the ratio of sine to cosine, or equivalently, the ratio of the y-coordinate to the x-coordinate:
\[\tan(θ) = \frac{\sin(θ)}{\cos(θ)} = \frac{y}{x}\]
For example, at 0 degrees, the coordinates are (1, 0), leading to:
\[\sin(0^\circ) = 0\]
\[\cos(0^\circ) = 1\]
\[\tan(0^\circ) = \frac{0}{1} = 0\]
At 90 degrees, the coordinates are (0, 1), resulting in:
\[\sin(90^\circ) = 1\]
\[\cos(90^\circ) = 0\]
\[\tan(90^\circ) = \frac{1}{0} \text{ (undefined)}\]
Continuing with other angles, at 180 degrees, the coordinates are (-1, 0), giving:
\[\sin(180^\circ) = 0\]
\[\cos(180^\circ) = -1\]
\[\tan(180^\circ) = \frac{0}{-1} = 0\]
At 270 degrees, the coordinates are (0, -1), leading to:
\[\sin(270^\circ) = -1\]
\[\cos(270^\circ) = 0\]
\[\tan(270^\circ) = \frac{-1}{0} \text{ (undefined)}\]
For angles in other quadrants, such as 217 degrees, the coordinates are found in the third quadrant, where both x and y values are negative. For 217 degrees, if the coordinates are (-4/5, -3/5), then:
\[\sin(217^\circ) = -\frac{3}{5}\]
\[\cos(217^\circ) = -\frac{4}{5}\]
\[\tan(217^\circ) = \frac{-\frac{3}{5}}{-\frac{4}{5}} = \frac{3}{4}\]
In the first quadrant, for an angle of 60 degrees, the coordinates are (1/2, √3/2), leading to:
\[\sin(60^\circ) = \frac{\sqrt{3}}{2}\]
\[\cos(60^\circ) = \frac{1}{2}\]
\[\tan(60^\circ) = \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \sqrt{3}\]
Understanding these relationships allows for easier calculations of trigonometric values using the unit circle, reinforcing the connection between angles and their corresponding coordinates.