To answer each question, refer to the following basic graphs. Which one is the graph of ƒ(x)=√x? What is its domain?
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
3. Functions
Intro to Functions & Their Graphs
Problem 16
Textbook Question
Determine the intervals of the domain over which each function is continuous. See Example 1.
 Verified step by step guidance
Verified step by step guidance1
Identify the given function and write it down explicitly to understand its form and any potential points of discontinuity.
Recall that polynomial functions are continuous everywhere, rational functions are continuous where the denominator is not zero, and root functions are continuous where the expression inside the root is defined (e.g., non-negative for even roots).
Find the domain of the function by determining where it is defined. For rational functions, set the denominator not equal to zero and solve for the variable. For root functions, set the radicand greater than or equal to zero and solve.
Use the domain to identify intervals where the function is continuous. The function is continuous on all intervals within its domain where no discontinuities (like division by zero or negative radicands) occur.
Express the intervals of continuity using interval notation, combining all continuous intervals found from the domain analysis.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Domain of a Function
The domain of a function is the set of all input values (x-values) for which the function is defined. Understanding the domain is essential because continuity can only be analyzed where the function exists. For example, functions involving square roots or denominators require restrictions to avoid undefined values.
Recommended video:

Domain Restrictions of Composed Functions
Continuity of a Function
A function is continuous at a point if the limit of the function as it approaches that point equals the function's value there. Continuity over an interval means the function has no breaks, jumps, or holes within that interval. Recognizing types of discontinuities helps in determining continuous intervals.
Recommended video:

Graphs of Common Functions
Types of Discontinuities
Discontinuities occur when a function is not continuous at a point. Common types include removable (holes), jump, and infinite discontinuities. Identifying these helps in pinpointing where continuity fails and thus in determining intervals where the function remains continuous.
Recommended video:
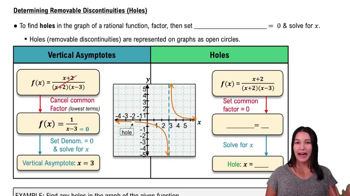
Determining Removable Discontinuities (Holes)

 5:2m
5:2mWatch next
Master Relations and Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
501
views
