Determine the system of equations illustrated in each graph. W...

Question

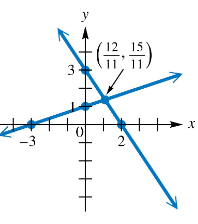
Determine the system of equations illustrated in each graph. Write equations in standard form.

Graph showing two intersecting lines with labeled axes and the intersection point at (12/11, 15/11).

Accepted Answer

Hey, everyone in this problem in standard form, we're asked to write the system of equations associated with the graph. And we have a graph with two straight lines that intersect at 1. answer choices, options A through D that each show a different combination of two equations. Now, looking back at our graph and we're gonna work through this one by one. OK. So we're gonna start with the first line, write out the equation and then move to the second, the first one we're gonna start with, it's the line that has the points zero, comma seven and negative four comma zero given. So let's recall, we can write the equation of a line as Y is equal to M X plus B. And this is the form of the equation we're gonna use to write it up. Now you can use point slope form as well. If you prefer that in this case, they're both gonna give you the same answer and they're both gonna be about the same amount of work. OK? So either one is fine. Now let's start, we have the points zero, comma seven and negative four comma zero. Now recall that the Y intercept is gonna be when X is equal to zero. And well, we have a 0.0 comma seven. So when X is equal to zero, Y is equal to seven. So why intercept is equal to seven? Which means that our B value is equal to seven? They recalled the B value in the equation Y equals M X plus B represents the Y intercept. And if you forget that you can always substitute in the point as well. If you substitute in the point with X equals zero, you just get Y is equal to B and the Y Y value in this case is seven. So now we have that Y is equal to M X. What we're gonna use our second point. So now we're gonna substitute in the point negative four comma zero. This gives us that zero is equal to M multiplied by negative four plus can move the seven to the left-hand side by subtracting it. And then dividing both sides by negative four to isolate M. We get M is equal to negative seven divided by negative four. Those two negatives will cancel. And we can write this as seven divided by four. So now we have that our equation is Y is equal to seven divided by four multiplied by X. What? Now remember the question is to write in standard form. So let's recall the standard form of a line. We wanna have X and Y on the left hand side, we want to have a constant on the right hand side and our answer choices don't have any fractions. So we want to eliminate our fractions as well. So we're gonna start by multiplying both sides by four to eliminate that fraction. We have four Y, it's equal to seven X plus oops, not plus seven, we have to multiply by four. So plus 28. Now we're gonna move the seven X to the left-hand side to put this in standard form, we have four, Y minus seven X is equal to 28. And this is the standard form of our line for that first um line of in the graph that we were given if we compare this to our answer choices, OK? We can see that we can already eliminate some of the options. A option A has that seven X being positive on the left hand side instead of negative. So we can eliminate that one. The rest of the answer choices have the correct equation negative seven X plus four Y is equal to 28. So we'll leave those ones for now. We'll move to the second equation and we'll figure out which is the correct answer choice. So moving to the next equation, we're given two points. OK? We're also given the intersection point, but we're just gonna use these other two points that's enough. And those are simpler to deal with. We have zero comma two and six comma zero. So let me write on the right hand side here. So I don't have to scroll away from the graph just yet if Y is equal to M X plus B and I'm gonna do this in green so that we can keep it separate from the other equation. And our points here is zero, comma two and six comma zero. So just like the other one we have that the Y intercept is gonna be equal to two. In this case, because when X is equal to zero, Y is equal to two, this tells us that our B value is equal to two. So we can write our equation as Y is equal to M X Y two, you can substitute in are other 0.6 comma zero that zero is equal to M multiplied by six plus two. We want to isolate and solve for M, we can move the two over to the left-hand side by subtracting and divide by six. We get that M is equal to negative two divided by six which we can simplify by dividing numerator and denominator by two to negative one third. So we have our M value, we can write our equation as Y is equal to negative one third, X plus two. And again, we want to write this in standard form, we're gonna multiply both sides by three. We have three, Y is equal to negative X plus six. We move the negative X to the left hand side by adding it. And we get that X plus three Y is equal the stick. OK. And that is that second equation that we were looking for for this system, we've eliminated option A option B has negative two Y instead of positive three Y, option D has positive two Y instead of positive three Y. So the correct answer here is option C A has a system of equations with both equations that we found. We have negative seven, X plus four, Y is equal to 28 X plus three Y is equal to six. Thanks everyone for watching. I hope this video helped see you in the next one.

Determine the system of equations illustrated in each graph. Write equations in standard form.

Key Concepts

Finding the Equation of a Line from Two Points

Converting to Standard Form of a Linear Equation

Interpreting Graphs to Identify Key Points

Watch next