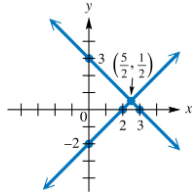
Determine the system of equations illustrated in each graph. Write equations in standard form.

Verified step by step guidance

1. Identify two points on the first line. From the graph, these points are (-8, 0) and (-4, 0).
2. Calculate the slope of the first line using the formula \(m = \frac{y_2 - y_1}{x_2 - x_1}\). Since both points have \(y=0\), the slope is \(m = 0\).
3. Write the equation of the first line in slope-intercept form: \(y = 0\). Convert this to standard form: \(y = 0\) or \$0x + y = 0$.
4. Identify two points on the second line. From the graph, these points are (0, 10) and (0, -3).
5. Calculate the slope of the second line using the formula \(m = \frac{y_2 - y_1}{x_2 - x_1}\). Since both points have \(x=0\), the slope is undefined, indicating a vertical line. The equation is \(x = 0\) in standard form.

Key Concepts

Finding the Equation of a Line from Intercepts

A line can be determined using its x- and y-intercepts by applying the intercept form of a linear equation. The formula is \( \frac{x}{a} + \frac{y}{b} = 1 \), where \(a\) and \(b\) are the x- and y-intercepts respectively. This form helps quickly write the equation when intercepts are known from the graph.

Converting to Standard Form of a Linear Equation

The standard form of a linear equation is \(Ax + By = C\), where A, B, and C are integers, and A ≥ 0. After finding the equation from intercepts or slope-intercept form, rearranging terms to this form is essential for consistency and comparison of linear equations.

Interpreting Graphs to Identify Systems of Equations

A system of equations consists of two or more linear equations graphed on the same coordinate plane. Understanding how to read points, intercepts, and slopes from the graph allows one to write each equation accurately and analyze their intersection points, which represent solutions to the system.