Graph the parabola 8 ( x + 1 ) = ( y − 2 ) 2 8\left(x+1\right)=\left(y-2\right)^2 8 ( x + 1 ) = ( y − 2 ) 2 , and find the focus point and directrix line.

Welcome back, everyone. Let's give this problem a try. So in this problem, we are asked to graph the parabola 8 times x plus one equals y minus 2 squared, and find the focus point and directrix line. Now what I noticed with this problem is we're dealing with a situation where the y variable is squared. And because of this, that means we're going to have some kind of sideways parabola on our graph. So what I can do is use the standard equation for a horizontal parabola, which is 4p times x minus h is equal to y minus k squared. Now from here I can extract the vertex of our parabola, and I noticed that this h corresponds with 1, but since we have a plus sign rather than a minus sign, that means h is going to be negative 1. Now I can see that this k corresponds with 2, and we have a minus sign there and there so this checks out. So all we need is the positive 2 for k. So the vertex of our parabola is going to be at negative 12, which on our graph we go back to negative 1 and up 2 will be right there. So that's the vertex. Now what I also need to do is find the focus and directrix and then graph the parabola. So to find the directrix and focus what I can do is use this 4p, I can set 4p equal to everything in front of the x minus h argument which is going to be this 8. So we're going to have that 4p is equal to 8. That can divide 4 on both sides, and 8 divided by 4 is 2, so that means our p value is equal to 2. Now notice we got a positive value, and because we got a positive p value that means our parabola is going to open to the right. Now this also tells us where our focus and directrix are. The focus points starting at the vertex is going to be 2 units to the right, because that's the direction that the parabola opens. So we can see that our focus point is going to be at the point 1, comma, 2, and that's our focus. Now what we need to find next is the directrix line, and the directrix line is opposite the direction that the parabola opens at a distance of p. So that means we're going to go back 1, 2 units to get our directrix line. So our directrix line is going to be at x equals negative 3, and this would be our directrix, and then what we found for the point over here would be our focus. So we have found the focus and directrix in this problem, and our last step is going to be to actually graph this parabola. And to graph the parabola, we can use the vertex, and we can go 2p units up and down to find the width. So 2p is the same thing as 2 times 2, which is 4, so I can go up 1, 2, 3, 4 units, which is actually gonna be somewhere up here. So we're actually past what we have on our graph here. It's gonna be if we extend this up, it would be at 6. So we go 4 units up, and then we can go 1, 2, 3, 4 units down. And what this is going to do is give us a parabola, which looks something like that. So this would be our parabola, and this would be the focus and directrix associated with this parabola as well. So that is how you can solve this problem. Hope you found this helpful. Let me know if you have any questions.

8. Conic Sections

Parabolas

College Algebra

8. Conic Sections

Parabolas

Struggling with College Algebra?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

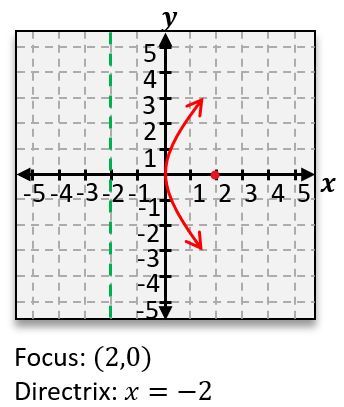
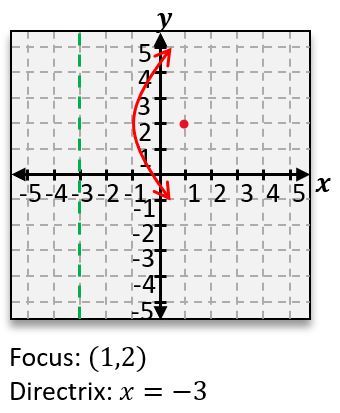
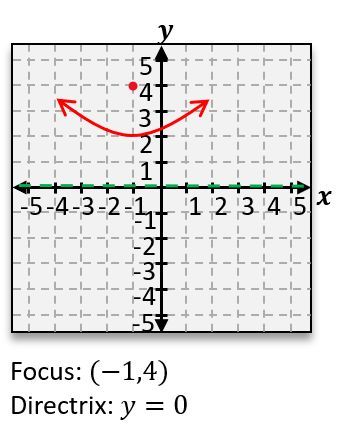
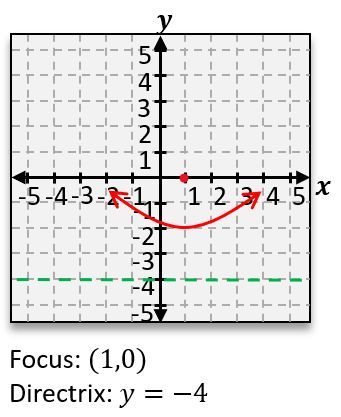
Graph the parabola $8\left(x+1\right)=\left(y-2\right)^2$ , and find the focus point and directrix line.

option a

option b

optiuon c

option d

Verified step by step guidance

Start by rewriting the given equation in the standard form of a parabola. The given equation is 8(x+1) = (y-2)^2. This is a horizontal parabola because the y-term is squared.

The standard form for a horizontal parabola is (y-k)^2 = 4p(x-h), where (h, k) is the vertex of the parabola. Compare this with the given equation to identify h, k, and p.

From the equation 8(x+1) = (y-2)^2, we can see that h = -1 and k = 2. The equation can be rewritten as (y-2)^2 = 8(x+1), which matches the standard form.

Identify the value of 4p from the equation. Here, 4p = 8, so p = 2. The focus of the parabola is located at (h+p, k) for a horizontal parabola.

The directrix of a horizontal parabola is a vertical line given by x = h - p. Use the values of h and p to find the equation of the directrix.

5:33m

Watch next

Master Parabolas as Conic Sections with a bite sized video explanation from Patrick

Start learning

Parabolas practice set

Problem sets built by lead tutors

Expert video explanations

Go to Practice

Struggling with College Algebra?

Graph the parabola 8(x+1)=(y−2)28\left(x+1\right)=\left(y-2\right)^28(x+1)=(y−2)2 , and find the focus point and directrix line.

Watch next

Parabolas practice set

Graph the parabola $8\left(x+1\right)=\left(y-2\right)^2$ , and find the focus point and directrix line.