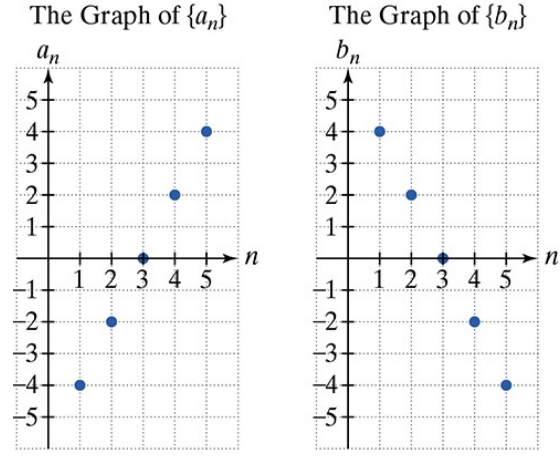
In Exercises 61–68, use the graphs of and to find each indicated sum.

${\sum }_{i=1}^5(a_i+3b_i)$

Verified step by step guidance

1. Step 1: Identify the values of the sequences \(a_n\) and \(b_n\) for \(n = 1, 2, 3, 4, 5\) from the graphs. For \(a_n\), read the y-values of the points at \(n=1, 2, 3, 4, 5\). For \(b_n\), do the same for the corresponding \(n\) values.
2. Step 2: Write down the values explicitly. For example, \(a_1 = \text{value from graph}\), \(a_2 = \text{value from graph}\), and so on, similarly for \(b_1, b_2, b_3, b_4, b_5\).
3. Step 3: Calculate each term inside the summation \(a_i + 3b_i\) for \(i = 1, 2, 3, 4, 5\). This means multiply each \(b_i\) by 3 and then add the corresponding \(a_i\).
4. Step 4: Sum all the calculated terms from Step 3 to find \(\sum_{i=1}^5 (a_i + 3b_i)\). This involves adding the five values obtained for each \(i\).
5. Step 5: Write the final expression for the sum, showing the addition of all terms explicitly, but do not compute the numerical total as per instructions.

Key Concepts

Sequences and Terms

A sequence is an ordered list of numbers, where each number is called a term. The term a_n represents the nth term of sequence a, and similarly b_n for sequence b. Understanding how to identify and interpret terms from graphs is essential for working with sequences.

Summation Notation (Sigma Notation)

Summation notation, represented by the Greek letter sigma (Σ), is a concise way to express the sum of a sequence of terms. For example, Σ from i=1 to 5 of (a_i + 3b_i) means adding the values of a_i plus three times b_i for i = 1 through 5.

Using Graphs to Extract Sequence Values

Graphs of sequences plot term indices on the x-axis and term values on the y-axis. To find specific terms like a_i or b_i, locate the point at x = i and read the corresponding y-value. This skill is crucial for evaluating sums involving terms from graphical data.