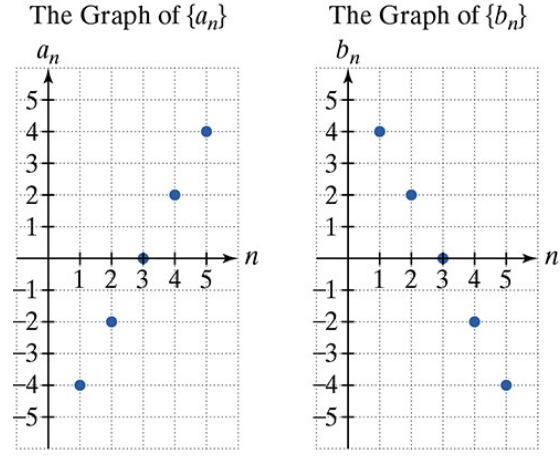
In Exercises 61–68, use the graphs of and to find each indicated sum.

${\sum }_{i=1}^5(a_i^2+1)$

Verified step by step guidance

1. Identify the values of the sequence \( a_n \) from the graph for \( n = 1 \) to \( n = 5 \). From the graph, the points are: \( a_1 = -2 \), \( a_2 = 0 \), \( a_3 = 2 \), \( a_4 = 4 \), and \( a_5 = 6 \).
2. Write the expression for the sum you need to find: \( \sum_{i=1}^5 (a_i^2 + 1) \). This means for each \( i \) from 1 to 5, you square the value of \( a_i \), then add 1, and finally sum all these results.
3. Calculate each term inside the sum separately: For each \( i \), compute \( a_i^2 + 1 \). For example, for \( i=1 \), calculate \( (-2)^2 + 1 \), for \( i=2 \), calculate \( 0^2 + 1 \), and so on.
4. After finding each term \( a_i^2 + 1 \), add all these values together to get the total sum.
5. Write the final sum as \( (a_1^2 + 1) + (a_2^2 + 1) + (a_3^2 + 1) + (a_4^2 + 1) + (a_5^2 + 1) \) and simplify if needed.

Key Concepts

Sequences and Terms

A sequence is an ordered list of numbers where each number is called a term, denoted as a_n. Understanding how to identify and interpret terms from a graph is essential, as each point corresponds to a term's value at a specific position n.

Summation Notation (Sigma Notation)

Summation notation, represented by the Greek letter Σ, is a concise way to express the sum of a sequence of terms. It includes an index of summation, lower and upper limits, and the general term to be summed, allowing efficient calculation of sums like Σ from i=1 to 5.

Evaluating Expressions Involving Sequence Terms

To find sums involving expressions like (a_i^2 + 1), you must first determine each term a_i from the graph, then square it, add 1, and finally sum all these values over the given range. This process combines understanding of sequences, algebraic operations, and summation.