Give the equations of any vertical, horizontal, or oblique asymptotes for the graph of each rational function. ƒ(x)=(x2+1)/(x2+9)
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
5. Rational Functions
Introduction to Rational Functions
Problem 95
Textbook Question
Use long division to rewrite the equation for g in the form quotient + remainder/divisor. Then use this form of the function's equation and transformations of f(x) = 1/x to graph g. g(x) = (2x+7)/(x+3)
 Verified step by step guidance
Verified step by step guidance1
Identify the dividend and divisor for the long division. Here, the dividend is the numerator polynomial \$2x + 7\( and the divisor is the denominator polynomial \)x + 3$.
Set up the long division by dividing the leading term of the dividend (\$2x\() by the leading term of the divisor (\)x\(). This gives the first term of the quotient: \)\frac{2x}{x} = 2$.
Multiply the entire divisor \(x + 3\) by the quotient term \$2\(, resulting in \)2(x + 3) = 2x + 6$.
Subtract this product from the original dividend: \((2x + 7) - (2x + 6)\). Simplify the subtraction to find the remainder.
Express the original function \(g(x)\) as the quotient plus the remainder over the divisor: \(g(x) = 2 + \frac{\text{remainder}}{x + 3}\). This form helps to analyze the graph by relating it to the parent function \(f(x) = \frac{1}{x}\) with transformations.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
13mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Polynomial Long Division
Polynomial long division is a method used to divide one polynomial by another, similar to numerical long division. It helps rewrite a rational function as a quotient plus a remainder over the divisor, simplifying the expression for analysis or graphing.
Recommended video:
Guided course

Introduction to Polynomials
Rational Functions and Their Graphs
A rational function is a ratio of two polynomials. Understanding its graph involves identifying asymptotes, intercepts, and behavior at infinity, which can be made clearer by rewriting the function using long division.
Recommended video:
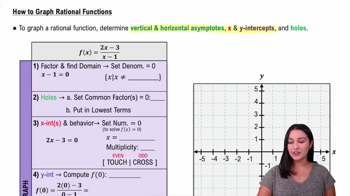
How to Graph Rational Functions
Transformations of the Parent Function f(x) = 1/x
The function f(x) = 1/x is a basic rational function with a hyperbola shape. Graphing related functions involves applying transformations like shifts, stretches, and reflections to this parent graph based on the rewritten form of the function.
Recommended video:

Domain & Range of Transformed Functions

 6:4m
6:4mWatch next
Master Intro to Rational Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
886
views
