Find the horizontal asymptote, if there is one, of the graph of each rational function. f(x)=12x/(3x2+1)
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
5. Rational Functions
Introduction to Rational Functions
Problem 79
Textbook Question
In Exercises 57–80, follow the seven steps to graph each rational function. f(x)=(3x2+x−4)/(2x2−5x)
 Verified step by step guidance
Verified step by step guidance1
Identify the domain of the function by finding the values of that make the denominator zero. Solve to find these values, since the function is undefined there.
Find the intercepts: For the y-intercept, evaluate if it is in the domain. For the x-intercepts, set the numerator equal to zero and solve to find the values of where .
Determine any vertical asymptotes by using the values of that make the denominator zero (from step 1), provided these values do not also make the numerator zero (which would indicate a hole instead).
Find the horizontal or oblique (slant) asymptote by comparing the degrees of the numerator and denominator polynomials. Since both are degree 2, divide the leading coefficients to find the horizontal asymptote.
Analyze the behavior of the function near the vertical asymptotes and at the ends of the domain by testing values of in each interval determined by the vertical asymptotes, and use this information to sketch the graph.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
17mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Rational Functions
A rational function is a ratio of two polynomials, expressed as f(x) = P(x)/Q(x). Understanding its domain, where the denominator Q(x) ≠ 0, is essential to avoid undefined values and to analyze the function's behavior.
Recommended video:
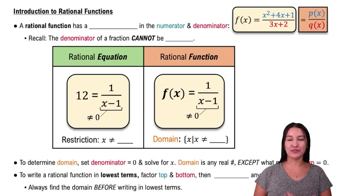
Intro to Rational Functions
Asymptotes
Asymptotes are lines that the graph of a function approaches but never touches. Vertical asymptotes occur where the denominator is zero, and horizontal or oblique asymptotes describe end behavior as x approaches infinity or negative infinity.
Recommended video:

Introduction to Asymptotes
Graphing Steps for Rational Functions
Graphing rational functions involves identifying domain restrictions, intercepts, asymptotes, and behavior near asymptotes, then plotting points to sketch the curve. Following a systematic approach ensures an accurate and complete graph.
Recommended video:
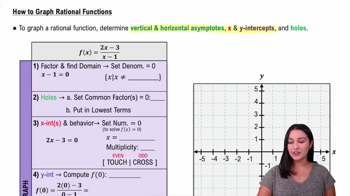
How to Graph Rational Functions

 6:4m
6:4mWatch next
Master Intro to Rational Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
790
views
