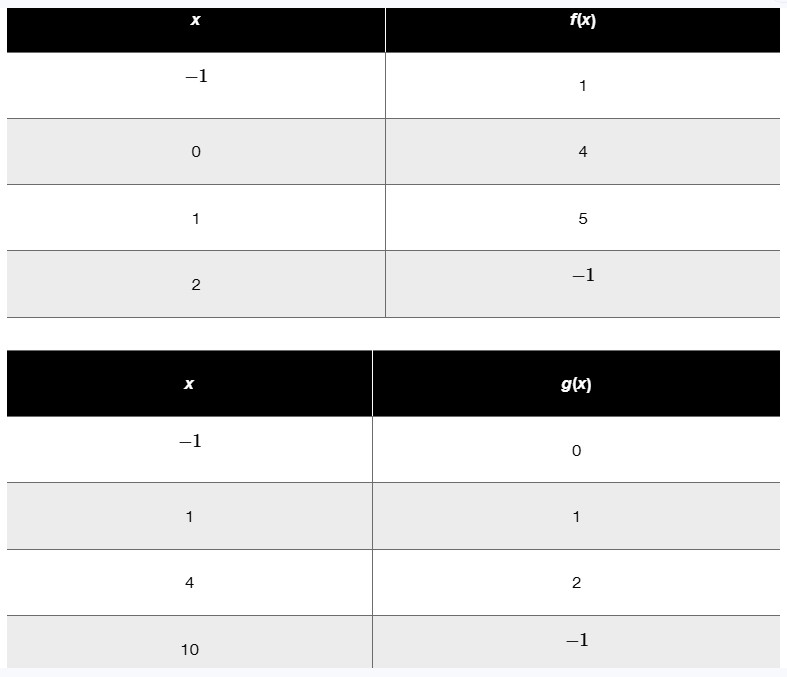
In Exercises 53–58, f and g are defined by the following tables. Use the tables to evaluate each composite function. (go f) (-1)

Verified step by step guidance

1. Identify the composite function to evaluate: (g \circ f)(-1), which means g(f(-1)).
2. Find the value of f(-1) from the first table. Look for the row where x = -1 and note the corresponding f(x) value.
3. Using the value found for f(-1), substitute it into the function g. This means you will look for g(f(-1)) in the second table by finding the row where x equals the value of f(-1).
4. Find the corresponding g(x) value from the second table for the x value found in the previous step.
5. The value you find for g(x) in the last step is the value of the composite function (g \circ f)(-1).

Key Concepts

Function Notation and Evaluation

Function notation, such as f(x), represents the output of a function f for an input x. Evaluating a function means finding the output value corresponding to a specific input by using the given function rule or table. For example, from the table, f(-1) = 1 means when x = -1, the output of f is 1.

Composite Functions

A composite function (g o f)(x) means applying function f first to x, then applying function g to the result of f(x). It is written as g(f(x)). To evaluate (g o f)(-1), first find f(-1), then use that output as the input for g.

Using Tables to Evaluate Functions

When functions are defined by tables, you find the output by locating the input value in the table and reading the corresponding output. For composite functions, use the output from the first function's table as the input for the second function's table.