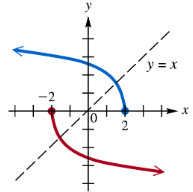
Determine whether each pair of functions graphed are inverses.

Verified step by step guidance

1. Step 1: Understand the concept of inverse functions. Two functions are inverses if their graphs are reflections of each other across the line \(y = x\). This means that every point \((a, b)\) on one function corresponds to a point \((b, a)\) on the other function.
2. Step 2: Identify the two functions on the graph. The orange curve represents one function, and the blue curve represents the other function. The green dashed line is the line \(y = x\), which acts as the mirror line for checking inverses.
3. Step 3: Check if the two functions are symmetric with respect to the line \(y = x\). Visually inspect if the orange and blue curves are mirror images of each other across the green dashed line.
4. Step 4: Look for corresponding points on the two functions. For example, if the orange function passes through \((4, 2)\), then the blue function should pass through \((2, 4)\) for them to be inverses.
5. Step 5: Conclude whether the two functions are inverses based on the symmetry and corresponding points. If the graphs are reflections across \(y = x\), then the functions are inverses; otherwise, they are not.

Key Concepts

Inverse Functions

Inverse functions reverse the effect of each other, meaning if f(x) maps x to y, then its inverse f⁻¹(x) maps y back to x. Graphically, two functions are inverses if reflecting one function's graph over the line y = x produces the other function's graph.

Line of Symmetry y = x

The line y = x acts as a mirror line for inverse functions. If two functions are inverses, their graphs are symmetric with respect to this line. Checking if one graph is the reflection of the other across y = x helps determine if they are inverses.

Graphical Verification of Inverses

To verify if two functions are inverses using their graphs, reflect one graph over the line y = x and see if it coincides with the other graph. This visual method provides an intuitive way to confirm inverse relationships without algebraic calculations.