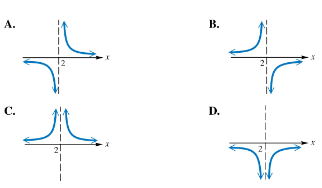
Work each problem. Choices A–D below show the four ways in which the graph of a rational function can approach the vertical line x=2 as an asymptote. Identify the graph of each rational function defined in parts (a) – (d). ƒ(x)=1/(x-2)^2

Verified step by step guidance

1. Identify the vertical asymptote by setting the denominator equal to zero: solve \( (x - 2)^2 = 0 \) which gives \( x = 2 \). This means the vertical asymptote is the line \( x = 2 \).
2. Analyze the behavior of the function near the vertical asymptote. Since the denominator is squared, \( (x - 2)^2 \), the function will approach infinity on both sides of \( x = 2 \) because the square makes the denominator always positive (except at \( x=2 \) where it is zero).
3. Check the sign of \( f(x) = \frac{1}{(x-2)^2} \) on intervals around \( x=2 \). For values slightly less than 2, \( (x-2)^2 \) is positive, so \( f(x) \) is positive and tends to \( +\infty \). For values slightly greater than 2, the same applies, so \( f(x) \) also tends to \( +\infty \).
4. Conclude that the graph approaches the vertical asymptote \( x=2 \) from above on both sides, meaning the function values increase without bound as \( x \) approaches 2 from the left and right.
5. Match this behavior to the correct graph choice among A–D, which should show the graph going to \( +\infty \) on both sides of the vertical asymptote at \( x=2 \).

Key Concepts

Vertical Asymptotes

A vertical asymptote occurs where a function approaches infinity or negative infinity as the input approaches a specific value, often where the denominator of a rational function is zero. For ƒ(x) = 1/(x-2)^2, the vertical asymptote is at x = 2 because the denominator becomes zero, causing the function to grow without bound.

Behavior Near Vertical Asymptotes

The behavior of a function near a vertical asymptote depends on the power of the factor in the denominator. If the factor is squared, like (x-2)^2, the function approaches positive infinity on both sides of the asymptote, resulting in the graph rising on both sides near x = 2.

Graphing Rational Functions

Graphing rational functions involves identifying asymptotes, intercepts, and end behavior. Understanding how the function behaves near vertical asymptotes helps in sketching the graph accurately, especially recognizing whether the graph approaches positive or negative infinity on each side of the asymptote.