Solve each polynomial inequality. Give the solution set in interval notation. (x - 4)(2x + 3)(3x - 1) ≥ 0
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
1. Equations & Inequalities
Linear Inequalities
Problem 39
Textbook Question
Solve each polynomial inequality. Give the solution set in interval notation. 2x3 - 7x2 ≥ 3 - 8x
 Verified step by step guidance
Verified step by step guidance1
First, rewrite the inequality so that all terms are on one side, setting the inequality to be greater than or equal to zero. This means subtracting 3 and adding 8x to both sides: \(2x^{3} - 7x^{2} - 3 + 8x \geq 0\).
Next, combine like terms to simplify the expression: \(2x^{3} - 7x^{2} + 8x - 3 \geq 0\).
Now, factor the polynomial expression on the left side if possible. Start by looking for rational roots using the Rational Root Theorem or by trial, then use polynomial division or synthetic division to factor the cubic polynomial into linear and/or quadratic factors.
After factoring, identify the critical points by setting each factor equal to zero and solving for \(x\). These points divide the number line into intervals.
Finally, test a value from each interval in the original inequality to determine where the inequality holds true. Use this information to write the solution set in interval notation, including endpoints where the inequality is 'greater than or equal to' zero.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
13mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Polynomial Inequalities
Polynomial inequalities involve expressions where a polynomial is compared to another value or polynomial using inequality symbols (>, <, ≥, ≤). Solving them requires finding the values of the variable that make the inequality true, often by analyzing the sign of the polynomial over different intervals.
Recommended video:
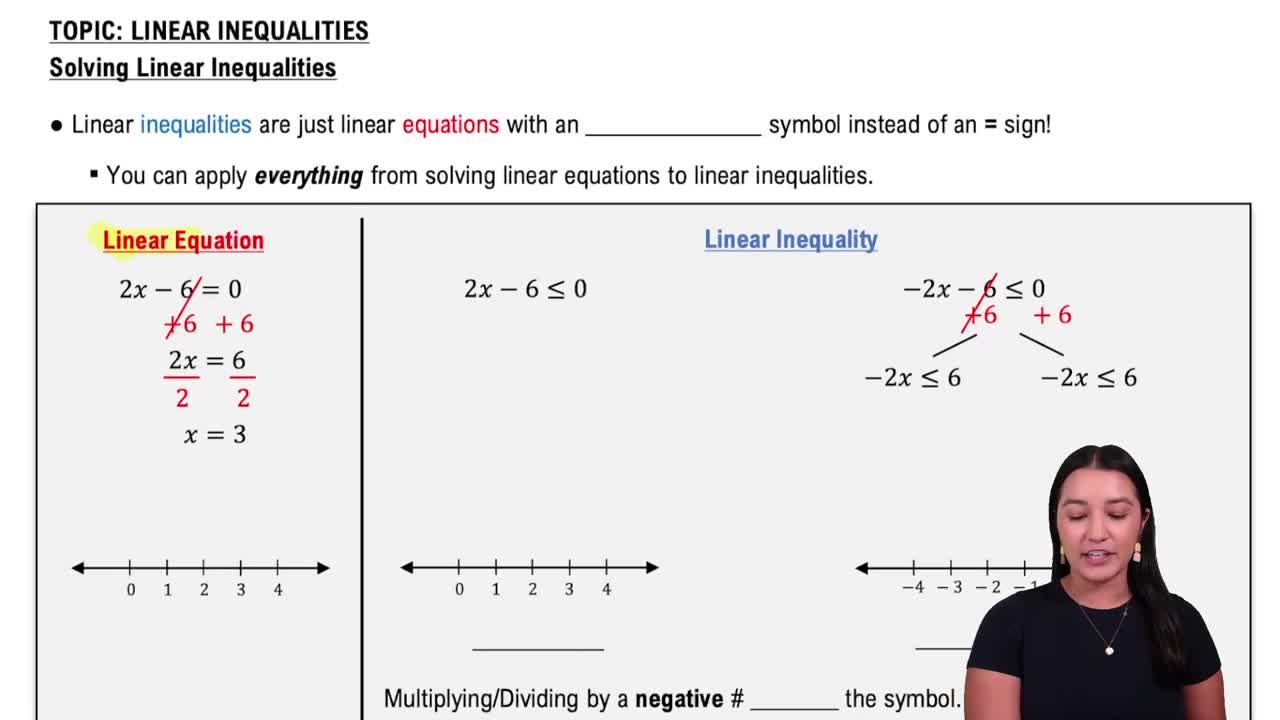
Linear Inequalities
Rearranging and Simplifying Inequalities
To solve polynomial inequalities, first rewrite the inequality so that one side is zero by moving all terms to one side. This simplification allows factoring or other methods to find critical points where the polynomial equals zero, which are essential for testing intervals.
Recommended video:
Guided course

Adding & Subtracting Unlike Radicals by Simplifying
Sign Analysis and Interval Notation
After finding the roots of the polynomial, use sign analysis to determine where the polynomial is positive or negative by testing values in intervals defined by the roots. The solution set is then expressed in interval notation, which concisely represents all values satisfying the inequality.
Recommended video:
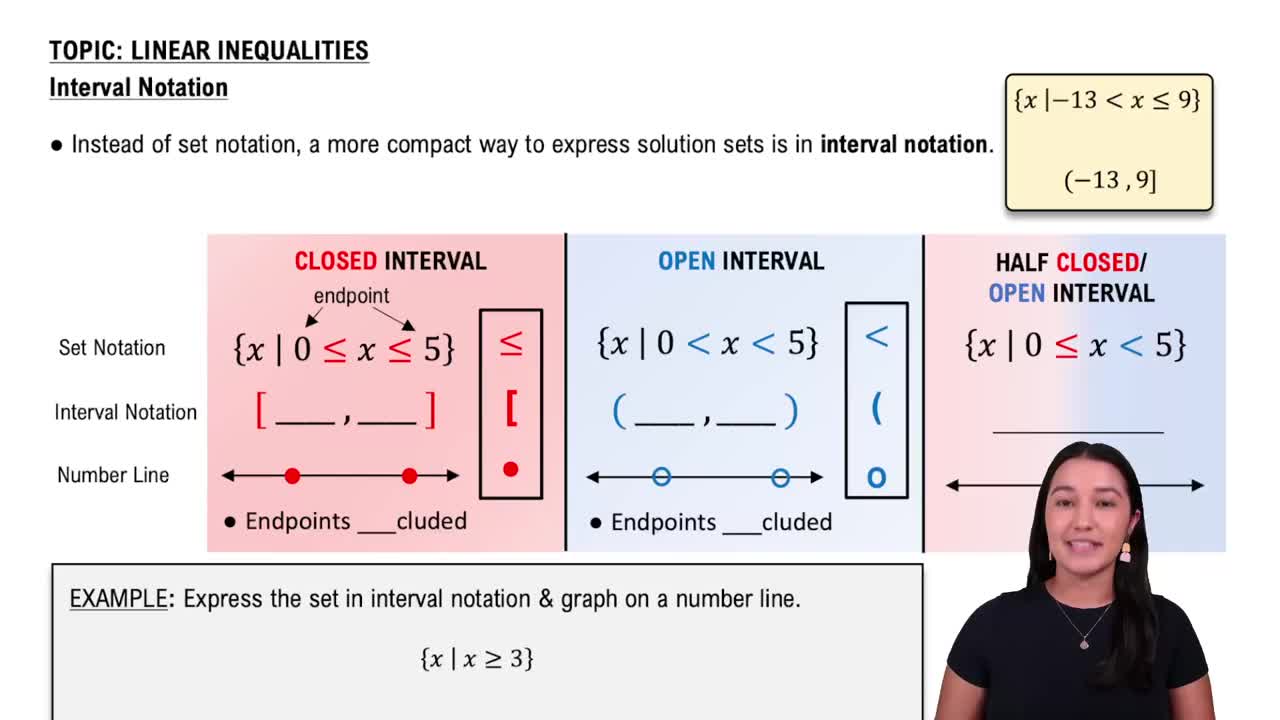
Interval Notation
Related Videos
Related Practice
Textbook Question
431
views


