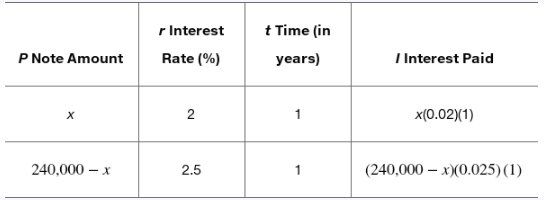
Solve each problem. See Example 4. Cody sells some property for \(240,000. The money will be paid off in two ways: a short-term note at 2% interest and a long-term note at 2.5%. Find the amount of each note if the total annual interest paid is \)5500.

Verified step by step guidance

1. Define variables for the amounts of the two notes. Let \(x\) be the amount of the short-term note at 2% interest, and \(y\) be the amount of the long-term note at 2.5% interest.
2. Write an equation representing the total amount of the property sold: \(x + y = 240000\).
3. Write an equation representing the total annual interest paid. The interest from the short-term note is \$0.02x\( and from the long-term note is \)0.025y$. The total interest is \(5500\), so the equation is \(0.02x + 0.025y = 5500\).
4. Use the first equation to express one variable in terms of the other, for example, \(y = 240000 - x\).
5. Substitute this expression for \(y\) into the interest equation and solve for \(x\). Once \(x\) is found, substitute back to find \(y\).

Key Concepts

Simple Interest Formula

Simple interest is calculated using the formula I = P × r × t, where I is the interest, P is the principal amount, r is the interest rate, and t is the time in years. Understanding this formula is essential to relate the interest earned from each note to its principal and rate.

System of Linear Equations

A system of linear equations involves two or more equations with multiple variables. Solving such systems helps find unknown values—in this case, the amounts of the short-term and long-term notes—by using methods like substitution or elimination.

Total Amount Constraint

The total amount of the property sold ($240,000) is split between two notes. This constraint forms one equation where the sum of the two note amounts equals the total sale price, providing a key relationship to solve the problem.