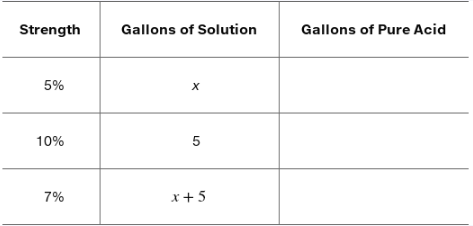
Solve each problem. See Example 3. How many gallons of a 5% acid solution must be mixed with 5 gal of a 10% solution to obtain a 7% solution?

Verified step by step guidance

1. Define the variable: Let \(x\) represent the number of gallons of the 5% acid solution to be mixed.
2. Write the expression for the amount of pure acid in each solution: The 5% solution contains \$0.05x$ gallons of acid, and the 10% solution contains \(0.10 \times 5\) gallons of acid.
3. Write the total volume of the mixture: The total volume after mixing is \(x + 5\) gallons.
4. Set up the equation for the concentration of the final mixture: The total amount of acid divided by the total volume equals 7%, so \(\frac{0.05x + 0.10 \times 5}{x + 5} = 0.07\).
5. Solve the equation for \(x\) by multiplying both sides by \((x + 5)\), expanding, combining like terms, and isolating \(x\).

Key Concepts

Mixture Problems

Mixture problems involve combining two or more solutions with different concentrations to form a new solution with a desired concentration. The key is to set up an equation based on the total amount of substance (e.g., acid) before and after mixing.

Concentration Percentage

Concentration percentage represents the amount of solute (acid) per total solution volume, expressed as a percent. Understanding how to convert percentages to decimals and use them in calculations is essential for solving mixture problems.

Setting Up and Solving Linear Equations

Solving mixture problems requires forming a linear equation that relates the volumes and concentrations of the solutions. This equation can then be solved algebraically to find the unknown quantity, such as the volume of one solution needed.