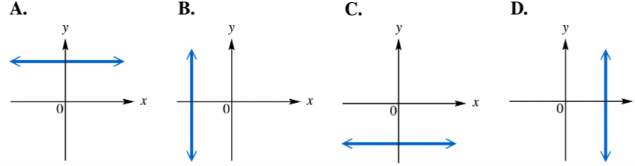
Match each equation with the sketch that most closely resembles its graph. y = 5

Verified step by step guidance

1. Identify the type of equation: The given equation is in the form \( y = c \), where \( c \) is a constant.
2. Understand the graph of the equation: The equation \( y = 5 \) represents a horizontal line.
3. Determine the position of the line: Since \( y = 5 \), the line is parallel to the x-axis and passes through the point (0, 5) on the y-axis.
4. Visualize the graph: The line will be horizontal and will intersect the y-axis at the point (0, 5).
5. Match with the sketch: Look for a graph that shows a horizontal line crossing the y-axis at 5.

Key Concepts

Constant Functions

A constant function is a type of function where the output value remains the same regardless of the input value. In the case of the equation y = 5, the function outputs the value 5 for every x-value. This results in a horizontal line on the graph, indicating that no matter how far you move along the x-axis, the y-value will always be 5.

Graphing Linear Equations

Graphing linear equations involves plotting points that satisfy the equation and connecting them to form a straight line. For the equation y = 5, the line is horizontal, which means it runs parallel to the x-axis. Understanding how to graph linear equations helps in visualizing the relationship between variables and interpreting their behavior.

Coordinate Plane

The coordinate plane is a two-dimensional surface defined by a horizontal axis (x-axis) and a vertical axis (y-axis). Each point on the plane is represented by an ordered pair (x, y). In the context of the equation y = 5, all points on the line will have a y-coordinate of 5, while the x-coordinate can take any real number value, illustrating the concept of a horizontal line in the coordinate system.