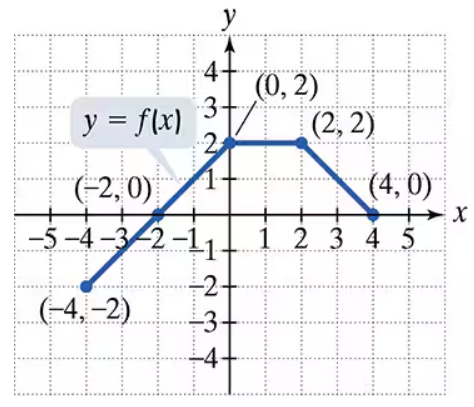
Use the graph of y = f(x) to graph each function g. g(x) = f(-x)
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
3. Functions
Common Functions
Problem 50
Textbook Question
Use the graph of y = f(x) to graph each function g. g(x) =(1/2) f(2x)
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the transformations applied to the function f(x). The given function g(x) = (1/2)f(2x) involves two transformations: a horizontal compression by a factor of 2 and a vertical scaling by a factor of 1/2.
Step 2: Start with the horizontal compression. The term f(2x) means that the graph of f(x) is compressed horizontally by a factor of 2. This means that every x-coordinate of the points on the graph of f(x) is divided by 2.
Step 3: Apply the vertical scaling. The term (1/2)f(2x) means that the graph of f(2x) is scaled vertically by a factor of 1/2. This means that every y-coordinate of the points on the graph of f(2x) is multiplied by 1/2.
Step 4: Combine the transformations. To graph g(x), first apply the horizontal compression to f(x), then apply the vertical scaling to the resulting graph.
Step 5: Plot the transformed points. For each point (x, y) on the graph of f(x), calculate the new coordinates as (x/2, y/2) and plot these points to create the graph of g(x).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Function Transformation
Function transformation refers to the process of altering the graph of a function through various operations, such as stretching, compressing, or shifting. In the case of g(x) = (1/2) f(2x), the function undergoes both a vertical compression by a factor of 1/2 and a horizontal compression by a factor of 1/2, affecting the overall shape and position of the graph.
Recommended video:

Domain & Range of Transformed Functions
Horizontal Scaling
Horizontal scaling involves changing the input values of a function, which affects how the graph is stretched or compressed along the x-axis. For g(x) = (1/2) f(2x), the '2' inside the function indicates that the graph of f(x) is compressed horizontally by a factor of 2, meaning that points on the graph will be closer together compared to the original function.
Recommended video:

Horizontal Parabolas
Vertical Scaling
Vertical scaling modifies the output values of a function, impacting the graph's height. In g(x) = (1/2) f(2x), the factor of 1/2 indicates a vertical compression, meaning that the output values of f(2x) are halved. This results in the graph being pulled closer to the x-axis, reducing its overall height while maintaining the same x-coordinates.
Recommended video:

Foci and Vertices of an Ellipse

 5:57m
5:57mWatch next
Master Graphs of Common Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
687
views
