Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
4. Polynomial Functions
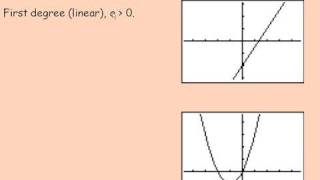
Understanding Polynomial Functions
Struggling with College Algebra?
Join thousands of students who trust us to help them ace their exams!Watch the first video
What Is a Polynomial?
Patrick Ford
Video duration:
1mPlay a video:
Related Videos
Related Practice