Use the given conditions to write an equation for each line in point-slope form and slope-intercept form. Slope = 8, passing through (4, −1)
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
2. Graphs of Equations
Lines
Problem 20
Textbook Question
Write an equation in slope-intercept form of a linear function f whose graph satisfies the given conditions. The graph of ƒ passes through (−2, 6) and is perpendicular to the line whose equation is x = -4.
 Verified step by step guidance
Verified step by step guidance1
Identify the given information: the function ƒ passes through the point \((-2, 6)\) and is perpendicular to the line \(x = -4\).
Recall that the line \(x = -4\) is a vertical line, which means its slope is undefined.
Since the line we want is perpendicular to a vertical line, it must be a horizontal line. Horizontal lines have a slope of 0.
Use the slope-intercept form of a line, which is \(y = m x + b\), where \(m\) is the slope and \(b\) is the y-intercept. Here, \(m = 0\), so the equation simplifies to \(y = b\).
Substitute the point \((-2, 6)\) into the equation \(y = b\) to find \(b\): since \(y = 6\), the equation of the line is \(y = 6\).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Slope-Intercept Form
The slope-intercept form of a linear equation is y = mx + b, where m represents the slope and b is the y-intercept. This form makes it easy to identify the slope and where the line crosses the y-axis, which is essential for graphing and writing linear equations.
Recommended video:
Guided course
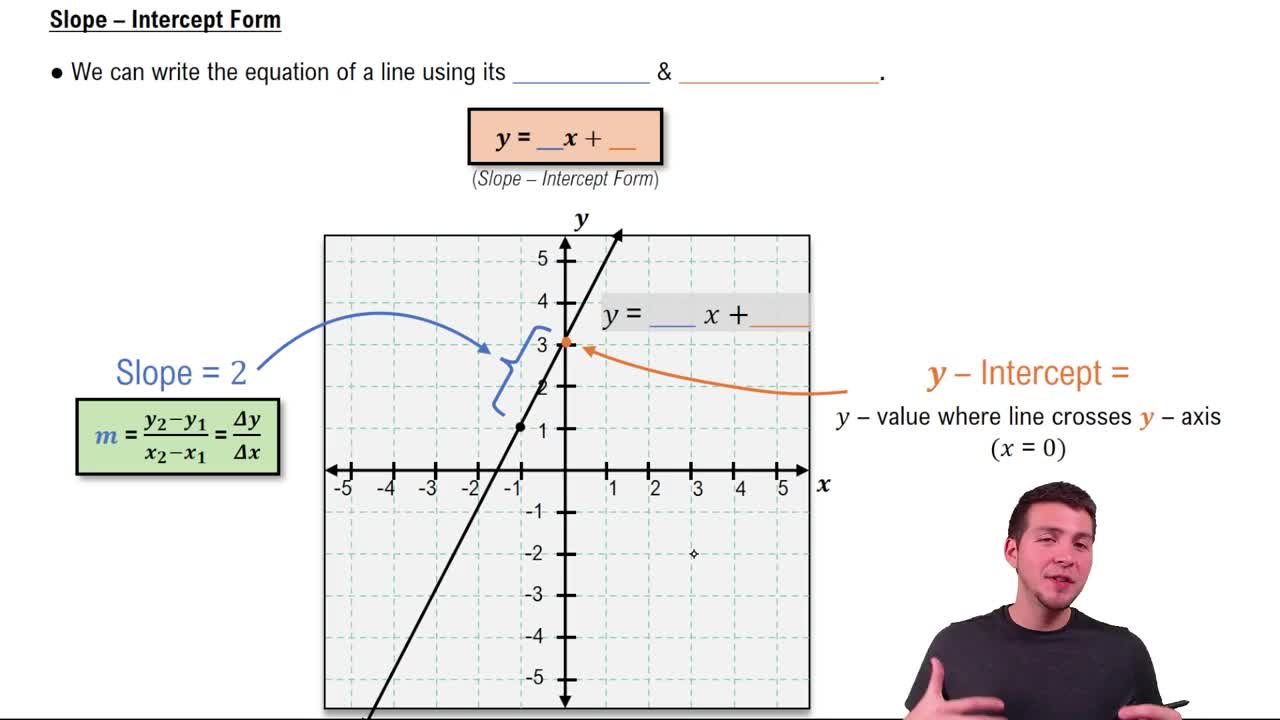
Slope-Intercept Form
Perpendicular Lines
Two lines are perpendicular if their slopes are negative reciprocals of each other. For vertical and horizontal lines, a vertical line has an undefined slope, and a line perpendicular to it is horizontal with a slope of zero. Understanding this helps determine the slope of the required line.
Recommended video:
Guided course

Parallel & Perpendicular Lines
Using a Point to Find the Equation
Given a point on the line and the slope, you can substitute these values into the slope-intercept form to solve for the y-intercept b. This step is crucial to write the complete equation of the line that meets the given conditions.
Recommended video:
Guided course

Finding Equations of Lines Given Two Points
Related Videos
Related Practice
Textbook Question
883
views
1
comments


