Graph each equation in a rectangular coordinate system. y = -2
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
2. Graphs of Equations
Lines
Problem 51
Textbook Question
Write an equation (a) in standard form and (b) in slope-intercept form for each line described. through (-1, 4), parallel to x+3y=5
 Verified step by step guidance
Verified step by step guidance1
Identify the slope of the given line by rewriting the equation \( x + 3y = 5 \) in slope-intercept form \( y = mx + b \). To do this, solve for \( y \): subtract \( x \) from both sides and then divide by 3.
Since the new line is parallel to the given line, it will have the same slope \( m \). Use this slope and the given point \( (-1, 4) \) to find the equation of the line.
Use the point-slope form of a line equation: \( y - y_1 = m(x - x_1) \), where \( (x_1, y_1) = (-1, 4) \) and \( m \) is the slope found in step 1.
Simplify the point-slope form equation to get the slope-intercept form \( y = mx + b \) by solving for \( y \). This completes part (b) of the problem.
Convert the slope-intercept form back to standard form \( Ax + By = C \) by moving all terms to one side and ensuring \( A, B, C \) are integers with \( A \geq 0 \). This completes part (a) of the problem.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Standard Form of a Linear Equation
The standard form of a linear equation is written as Ax + By = C, where A, B, and C are integers, and A should be non-negative. This form is useful for identifying intercepts and for certain algebraic manipulations. Converting an equation to this form often involves rearranging terms and clearing fractions.
Recommended video:
Guided course

Standard Form of Line Equations
Slope of a Line and Parallel Lines
The slope of a line measures its steepness and is calculated as the ratio of the change in y to the change in x (rise over run). Lines that are parallel have identical slopes. To find the slope of a line given in standard form, you can rewrite it in slope-intercept form or use the formula -A/B.
Recommended video:
Guided course

Parallel & Perpendicular Lines
Slope-Intercept Form of a Linear Equation
The slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept. This form clearly shows the slope and where the line crosses the y-axis, making it easy to graph and understand the line's behavior. It is often derived by solving the equation for y.
Recommended video:
Guided course
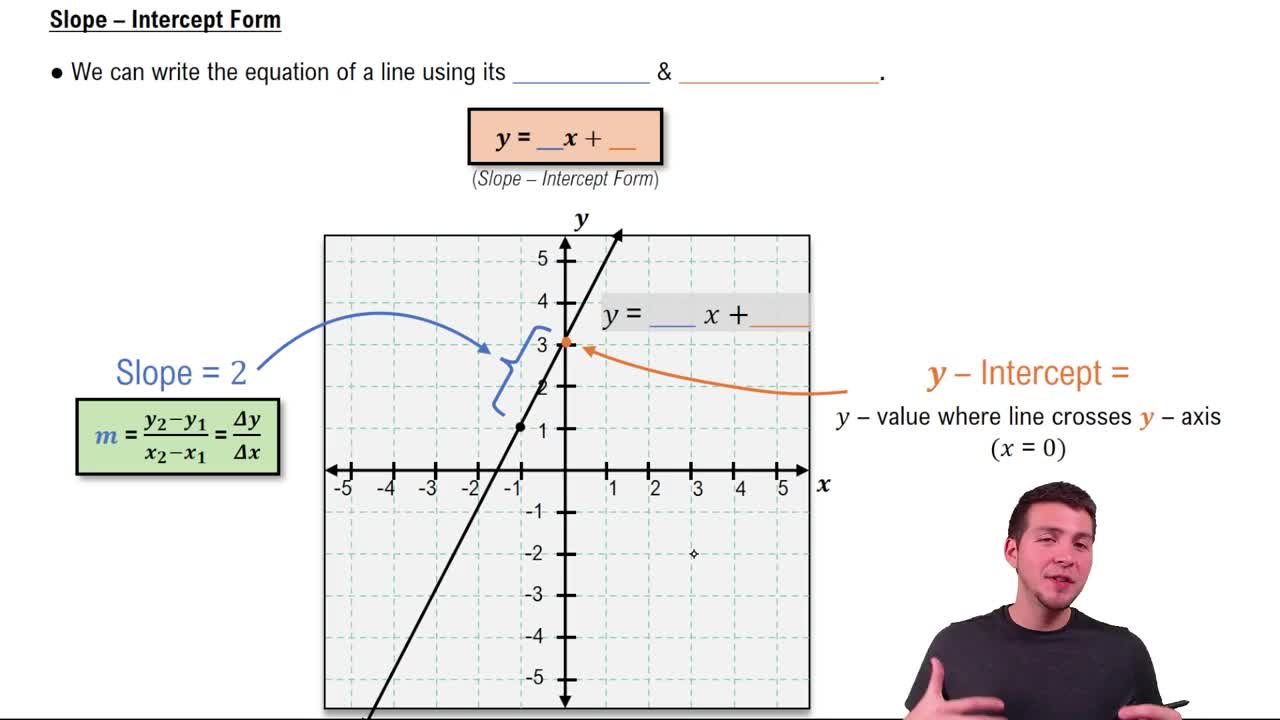
Slope-Intercept Form
Related Videos
Related Practice
Textbook Question
1186
views


