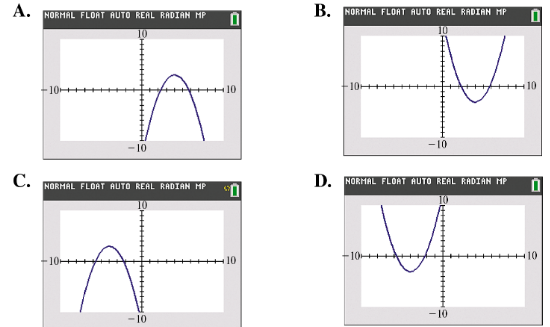
Consider the graph of each quadratic function.
a) Give the domain and range.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:



 7:42m
7:42mMaster Properties of Parabolas with a bite sized video explanation from Patrick
Start learning