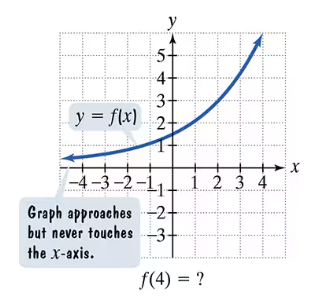
In Exercises 77–92, use the graph to determine a. the function's domain; b. the function's range; c. the x-intercepts, if any; d. the y-intercept, if any; and e. the missing function values, indicated by question marks, below each graph.

Verified step by step guidance

1. Step 1: Determine the domain of the function by looking at the x-values for which the graph is defined. Since the graph extends from negative infinity to positive 4 (and beyond), the domain includes all real numbers less than or equal to 4. Write the domain as \((-\infty, 4]\).
2. Step 2: Determine the range of the function by observing the y-values the graph takes. The graph approaches the x-axis (y=0) but never touches it, and it increases without bound as x increases. So, the range is all y-values greater than 0, written as \((0, \infty)\).
3. Step 3: Identify the x-intercepts by finding where the graph crosses the x-axis (where \(y=0\)). Since the graph approaches but never touches the x-axis, there are no x-intercepts.
4. Step 4: Identify the y-intercept by finding where the graph crosses the y-axis (where \(x=0\)). From the graph, observe the y-value at \(x=0\) and note it as the y-intercept.
5. Step 5: Find the missing function value \(f(4)\) by locating \(x=4\) on the graph and reading the corresponding y-value. This value is the output of the function at \(x=4\).

Key Concepts

Domain of a Function

The domain of a function is the set of all possible input values (x-values) for which the function is defined. In a graph, it corresponds to the horizontal extent of the curve. Understanding the domain helps determine where the function exists and can be evaluated.

Range of a Function

The range of a function is the set of all possible output values (y-values) that the function can produce. On a graph, it is the vertical spread of the curve. Knowing the range is essential to understand the behavior and limits of the function's outputs.

Intercepts and Asymptotes

Intercepts are points where the graph crosses the axes: x-intercepts occur where y=0, and y-intercepts where x=0. An asymptote is a line the graph approaches but never touches, indicating limits of the function. Recognizing these helps analyze function behavior and solve for missing values.