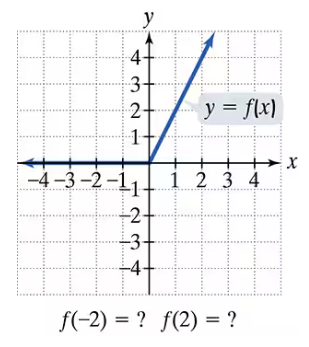
In Exercises 77–92, use the graph to determine a. the function's domain; b. the function's range; c. the x-intercepts, if any; d. the y-intercept, if any; and e. the missing function values, indicated by question marks, below each graph.

Verified step by step guidance

1. Step 1: Determine the domain of the function by identifying all the x-values for which the function is defined. From the graph, observe the segment starts at x = 0 and goes to x = 2, so the domain includes values from 0 to 2. Since the graph does not show values for x < 0, the domain is \([0, 2]\).
2. Step 2: Determine the range of the function by looking at the y-values that the function takes on the graph. The function starts at y = 0 when x = 0 and increases linearly to y = 4 when x = 2, so the range is \([0, 4]\).
3. Step 3: Find the x-intercepts by identifying points where the graph crosses the x-axis (where \(y=0\)). The graph passes through the origin (0,0), so the x-intercept is at \(x=0\).
4. Step 4: Find the y-intercept by identifying where the graph crosses the y-axis (where \(x=0\)). The graph passes through (0,0), so the y-intercept is \(y=0\).
5. Step 5: Determine the missing function values \(f(-2)\) and \(f(2)\). Since the graph is only defined from \(x=0\) to \(x=2\), \(f(-2)\) is not defined based on the graph. For \(f(2)\), look at the point on the graph at \(x=2\), which corresponds to \(y=4\), so \(f(2) = 4\).

Key Concepts

Domain of a Function

The domain of a function is the set of all possible input values (x-values) for which the function is defined. It is important to analyze the graph to see where the function exists along the x-axis, including any endpoints or breaks in the graph.

Range of a Function

The range of a function is the set of all possible output values (y-values) that the function can produce. By examining the graph, one can determine the minimum and maximum y-values covered by the function, including any gaps or limits.

Intercepts of a Function

Intercepts are points where the graph crosses the axes. The x-intercepts occur where the function equals zero (y=0), and the y-intercept occurs where the input is zero (x=0). Identifying these points helps understand the function's behavior and solve for missing values.