Solve each inequality. Give the solution set in interval notation. -4≤(x+1)/2≤5
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
1. Equations & Inequalities
Linear Inequalities
Problem 37
Textbook Question
Solve each inequality. Give the solution set in interval notation.
 Verified step by step guidance
Verified step by step guidance1
Start by understanding that the inequality involves an absolute value: \(|5 - 3x| \leq 7\). Recall that \(|A| \leq B\) means \(-B \leq A \leq B\) for any real numbers \(A\) and \(B \geq 0\).
Apply this property to the inequality: write it as a compound inequality: \(-7 \leq 5 - 3x \leq 7\).
Next, solve the left part of the compound inequality: \(-7 \leq 5 - 3x\). Subtract 5 from both sides to isolate the term with \(x\): \(-7 - 5 \leq -3x\), which simplifies to \(-12 \leq -3x\).
Divide both sides of the inequality by \(-3\) to solve for \(x\). Remember that dividing by a negative number reverses the inequality sign: \(\frac{-12}{-3} \geq x\), which simplifies to \(4 \geq x\) or \(x \leq 4\).
Now solve the right part of the compound inequality: \(5 - 3x \leq 7\). Subtract 5 from both sides: \(-3x \leq 2\). Divide both sides by \(-3\), reversing the inequality sign: \(x \geq -\frac{2}{3}\). Combine both parts to write the solution set in interval notation.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Absolute Value Inequalities
Absolute value inequalities involve expressions where the absolute value of a variable or expression is compared to a number. To solve |A| ≤ B, where B ≥ 0, rewrite it as -B ≤ A ≤ B, converting it into a compound inequality that can be solved using standard algebraic methods.
Recommended video:
Linear Inequalities
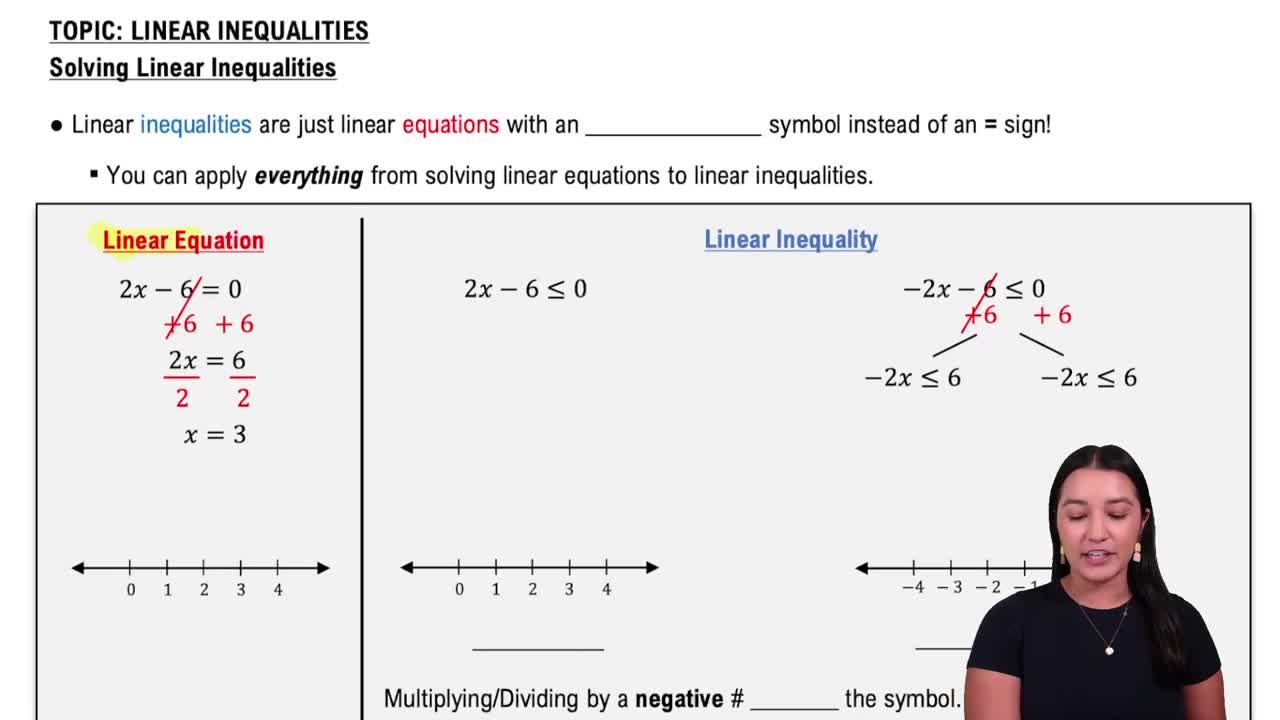
Solving Linear Inequalities
Solving linear inequalities requires isolating the variable on one side while maintaining the inequality's direction. When multiplying or dividing by a negative number, the inequality sign must be reversed. Solutions are often expressed as intervals or inequalities.
Recommended video:

Linear Inequalities
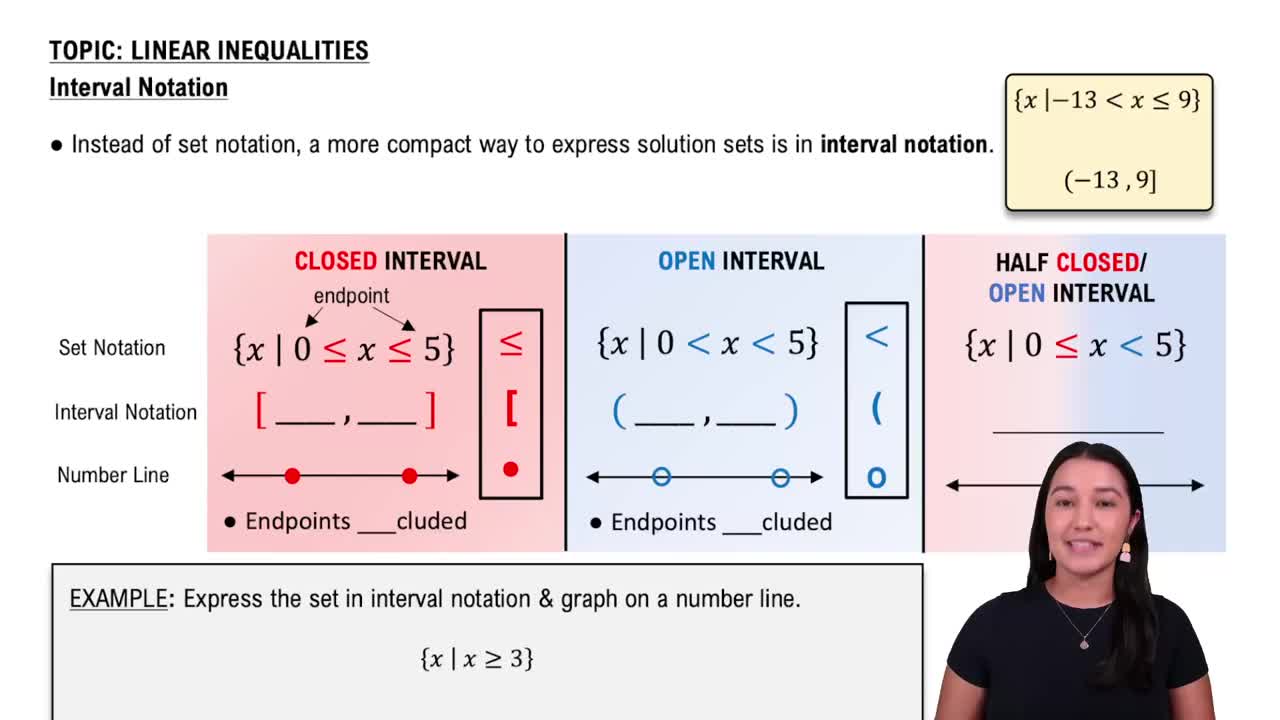
Interval Notation
Interval notation is a concise way to represent sets of numbers that satisfy inequalities. It uses parentheses () for values not included and brackets [] for values included. For example, [a, b] represents all numbers between a and b, including both endpoints.
Recommended video:
Interval Notation
Related Videos
Related Practice
Textbook Question
714
views


