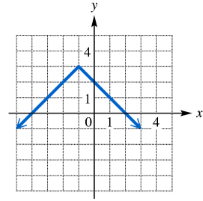
Each of the following graphs is obtained from the graph of ƒ(x)=|x| or g(x)=√x by applying several of the transformations discussed in this section. Describe the transformations and give an equation for the graph.

Verified step by step guidance

1. Step 1: Identify the base function. The graph resembles the shape of the absolute value function \(f(x) = |x|\), which has a 'V' shape with its vertex at the origin (0,0).
2. Step 2: Observe the vertex shift. The vertex of the graph is at \((-3, 5)\) instead of at the origin, indicating a horizontal shift 3 units to the left and a vertical shift 5 units up.
3. Step 3: Analyze the slopes of the lines. The left side of the graph has a positive slope of 1, and the right side has a negative slope of -2, which means the right side is steeper than the left side. This suggests a vertical stretch by a factor of 2 on the right side and no stretch on the left side.
4. Step 4: Write the piecewise function. Since the graph is based on \(|x|\), which is defined as \(f(x) = -x\) for \(x < 0\) and \(f(x) = x\) for \(x \\geq 0\), apply the transformations:
5. For \(x < -3\), the function is \(y = (x + 3) + 5\) (shifted left and up). For \(x \\geq -3\), the function is \(y = -2(x + 3) + 5\) (shifted left and up, and vertically stretched by 2 with reflection).

Key Concepts

Absolute Value Function

The absolute value function, f(x) = |x|, produces a V-shaped graph with its vertex at the origin. It outputs the distance of x from zero, always non-negative. Understanding its basic shape helps in identifying transformations like shifts, reflections, and stretches.

Transformations of Functions

Transformations include shifts (horizontal and vertical), reflections (across axes), stretches, and compressions. These changes alter the graph's position, orientation, or size. Recognizing how each transformation affects the graph is essential for writing the new equation.

Piecewise Linear Functions

A piecewise linear function is defined by different linear expressions over intervals. The graph in the image shows two linear segments joined at a vertex, indicating a transformation of the absolute value function. Understanding piecewise definitions helps in expressing the transformed function accurately.