5. Rational Functions

Asymptotes

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

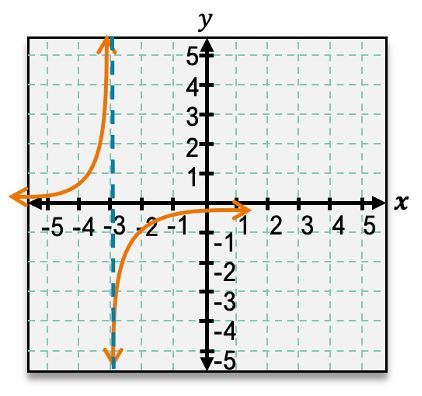
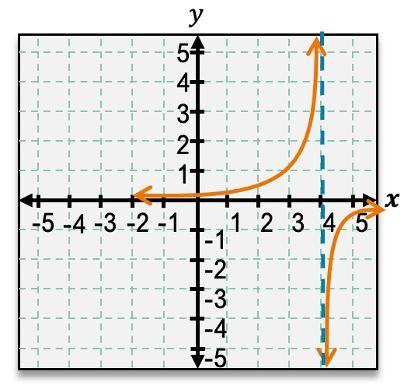
Based only on the vertical asymptotes, which of the following graphs could be the graph of the given function? $f\left(x\right)=\frac{x^2-4x}{x^2-x-12}$

Graph showing vertical asymptotes at x=-4 and x=3 for the function f(x).

Graph showing a vertical asymptote at x=-3 for the function f(x).

Graph showing vertical asymptotes at x=4 for the function f(x).

Verified step by step guidance

Identify the vertical asymptotes of the function by setting the denominator equal to zero: $x^2 - x - 12 = 0$.

Factor the quadratic equation in the denominator: $x^2 - x - 12 = (x - 4)(x + 3)$.

Set each factor equal to zero to find the values of $x$ that make the denominator zero: $x - 4 = 0$ and $x + 3 = 0$.

Solve these equations to find the vertical asymptotes: $x = 4$ and $x = -3$.

Compare the vertical asymptotes $x = 4$ and $x = -3$ with the graphs provided to determine which graph has these asymptotes.

Master Introduction to Asymptotes with a bite sized video explanation from Patrick

Problem sets built by lead tutors

Expert video explanations

Based only on the vertical asymptotes, which of the following graphs could be the graph of the given function? f(x)=x2−4xx2−x−12f\left(x\right)=\frac{x^2-4x}{x^2-x-12}f(x)=x2−x−12x2−4x