Sketch the graph of the function f(x)=1x2f\left(x\right)=\frac{1}{x^2}f(x)=x21. Identify the asymptotes on the graph.

Vertical Asymptote: x = 0 x=0 x = 0 , Horizontal Asymptote: y = 0 y=0 y = 0

Sketch the graph of the function f ( x ) = 1 x 2 f\left(x\right)=\frac{1}{x^2} f ( x ) = x 2 1 . Identify the asymptotes on the graph.

Hey everyone. Here we're asked to sketch the graph of the function 1 over x squared and then identify the asymptotes on the graph. So let's go ahead and start by looking at a table of points and determining where we can plot some points on our graph and what the behavior of our curves might be. So I'm going to start with the point x equals 1 and go ahead and plug that into my function. So plugging that in, I have 1 over 1 squared, which we know is just 1. So I can go ahead and plot this point on my graph, 11. Now as x gets larger and larger, we need to figure out what's happening here. So taking a look at x equals 2, now plugging that into our function, I'll get 1 over 2 squared which we know is just 1 over 4. So we see that it's getting even a little bit smaller and I can go ahead and try to sketch that point on my graph even though I don't have the exact point available to me. Now, let's go ahead and look at x equals 3. Now, if I plug that into my function I get 1 over 3 squared which is just 1 over 9 which is an even smaller fraction than 1 over 4. So I know that it's getting even smaller. If I even take it up to 10 for x, that gives me 1 over 10 squared, which is 1 over 100 or simply 0.01, which we know is a really small number. So we see what's happening over here as x gets larger and larger is that we're getting really, really close to the x axis, getting really close to 0, but not quite touching it. Now let's go ahead and look at what's happening on the other side of our function in between 0 and 1. So in between 0 and 1, we can take a look at the point 0.1. And if I plug that in, I get 1 over 0.1 squared, which is 1 over 0.01, which is actually just 100 if I put that in my calculator. Now we see that that's getting really, really large up here. It's going to be somewhere all the way up there. So that tells me that I'm going to be getting really close to my y axis as I get closer to x equals 0, but not quite touching it. Okay. Now I have the general shape of that side, but what's happening when x is negative? So let's take a look at x equals negative one. Now if I plug negative one into my function, I get one over negative one squared, which is just one over 1, which we know is just 1. So this is a point I can go ahead and plot my graph at negative one, one. Then if I take it into more and more negative, if I go further that direction on my x axis to x equals negative 10, I would get 1 over negative 10 squared, which would end up just being 1 over positive 100, which is really just 0.01, which is the same thing we actually got with positive 10. So we're going to see the same thing happening over here. We're going to be getting really, really close to the x axis but not quite touching it. Now finally, let's look between a 0 and a negative one and take a look at negative point 0.1. So finally, plugging that into my function, one over negative 0.1 squared gives me 1 over 0.01, which again is just 100, the same thing we got with positive 0.1. So again, we're going to be getting a really high up here, getting close to that y axis, but not quite touching it. So looking at the basic shapes of my graph, where are our asymptotes going to be? Well, we see that we're getting really close to the x axis on either side here. So that tells me that I have a horizontal asymptote right on my x axis at x equals 0, so or at y equals 0. So I have a horizontal asymptote there that I'm going to highlight just so that it's easier to see right at y equals 0. Now also looking at the other sides of my graph, I see that they're getting really close to the y axis from either side but not quite touching it, which tells me that I'm dealing with yet another asymptote, this time a vertical asymptote right on my y axis at x equals 0 that I'm again going to highlight just so that it's easier to see. Now, you might notice that these are the exact same asymptotes we saw with our function one over x. And we do have the same asymptotes, but now we see that both of my curves are positive even when x is negative just because now x is squared. So that's all we need to do for this function. Thanks for watching and I'll see you in the next video.

Sketch the graph of the function f ( x ) = 1 x 2 f\left(x\right)=\frac{1}{x^2} f ( x ) = x 2 1 . Identify the asymptotes on the graph.

Vertical Asymptote: x = 0 x=0 x = 0 , Horizontal Asymptote: y = 0 y=0 y = 0

Vertical Asymptote: x = 0 x=0 x = 0 , Horizontal Asymptote: None

Vertical Asymptote: x = 0 x=0 x = 0 , Horizontal Asymptote: y = 0 y=0 y = 0

Vertical Asymptote: x = 1 x=1 x = 1 , Horizontal Asymptote: y = 0 y=0 y = 0

5. Rational Functions

Asymptotes

College Algebra

5. Rational Functions

Asymptotes

Struggling with College Algebra?

Join thousands of students who trust us to help them ace their exams!

Multiple Choice

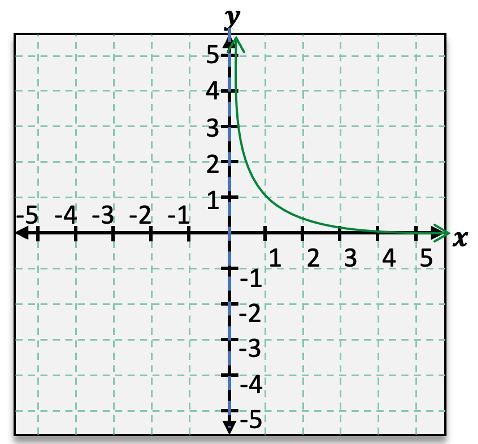
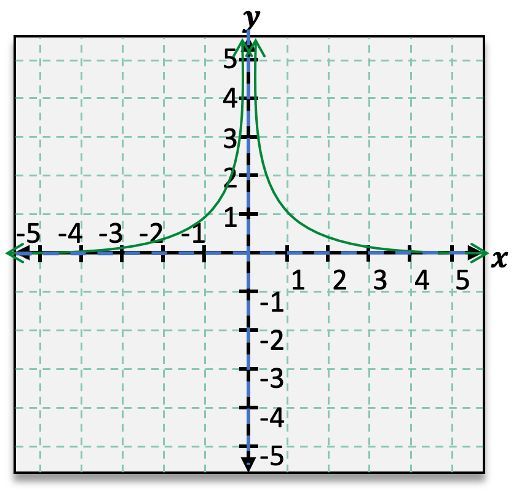
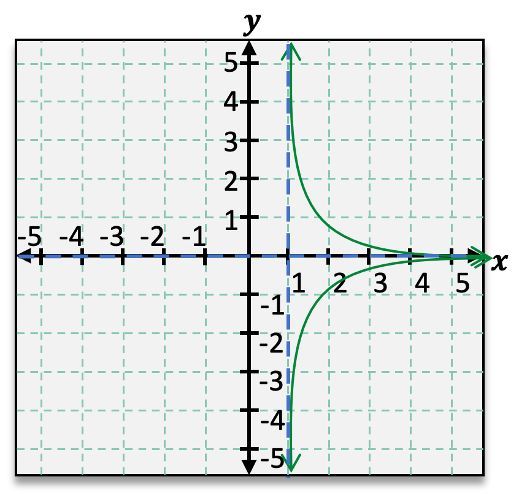
Sketch the graph of the function $f$\left$(x$\right$)=$\frac{1}{x^2}$$ . Identify the asymptotes on the graph.

Graph of f(x)=1/x^2 showing vertical asymptote at x=0 and horizontal asymptote at y=0.

Vertical Asymptote: $x=0$ , Horizontal Asymptote: None

Graph of f(x)=1/x^2 with vertical asymptote at x=0 and no horizontal asymptote.

Vertical Asymptote: $x=0$ , Horizontal Asymptote: $y=0$

Graph of f(x)=1/x^2 illustrating vertical asymptote at x=0 and horizontal asymptote at y=0.

Vertical Asymptote: $x=0$ , Horizontal Asymptote: $y=0$

Graph of f(x)=1/x^2 depicting vertical asymptote at x=1 and horizontal asymptote at y=0.

Vertical Asymptote: $x=1$ , Horizontal Asymptote: $y=0$

Verified step by step guidance

The function given is $ f(x) = \frac{1}{x^2} $. This is a rational function where the numerator is a constant and the denominator is a quadratic expression.

Identify the vertical asymptote by setting the denominator equal to zero. Since the denominator is $ x^2 $, set $ x^2 = 0 $. Solving this gives $ x = 0 $. Therefore, there is a vertical asymptote at $ x = 0 $.

To find the horizontal asymptote, consider the behavior of $ f(x) $ as $ x $ approaches infinity. As $ x \to \infty $ or $ x \to -\infty $, $ \frac{1}{x^2} \to 0 $. Thus, the horizontal asymptote is $ y = 0 $.

The graph of $ f(x) = \frac{1}{x^2} $ is symmetric about the y-axis because it is an even function. This means the graph will look the same on both sides of the y-axis.

In the graph, as $ x $ approaches 0 from the positive or negative side, $ f(x) $ approaches infinity, confirming the vertical asymptote at $ x = 0 $. As $ x $ moves away from zero in either direction, $ f(x) $ approaches zero, confirming the horizontal asymptote at $ y = 0 $.

6:24m

Watch next

Master Introduction to Asymptotes with a bite sized video explanation from Patrick

Asymptotes practice set

Problem sets built by lead tutors

Expert video explanations

Struggling with College Algebra?

Sketch the graph of the function f(x)=1x2f\(\left\)(x\(\right\))=\(\frac{1}{x^2}\)f(x)=x21. Identify the asymptotes on the graph.

Watch next

Asymptotes practice set

Sketch the graph of the function $f\(\left\)(x\(\right\))=\(\frac{1}{x^2}\)$ . Identify the asymptotes on the graph.