In Exercises 27 - 36, find (if possible) the following matrices: a. AB b. BA 1 2 2 - 3 1 - 1 - 1 1 A = B = 1 1 - 2 1 5 4 10 5

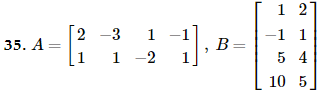
Verified step by step guidance

1. Step 1: Identify the dimensions of matrices A and B. Matrix A is a 2x4 matrix (2 rows, 4 columns), and matrix B is a 4x2 matrix (4 rows, 2 columns).
2. Step 2: To find the product AB, check if the number of columns in A equals the number of rows in B. Since A is 2x4 and B is 4x2, multiplication AB is possible and the resulting matrix will be 2x2.
3. Step 3: To find the product BA, check if the number of columns in B equals the number of rows in A. Since B is 4x2 and A is 2x4, multiplication BA is possible and the resulting matrix will be 4x4.
4. Step 4: Calculate each element of the product AB by taking the dot product of the rows of A with the columns of B. For example, the element in the first row and first column of AB is calculated as: $A[1,1]*B[1,1]+A[1,2]*B[2,1]+A[1,3]*B[3,1]+A[1,4]*B[4,1]$.
5. Step 5: Similarly, calculate each element of the product BA by taking the dot product of the rows of B with the columns of A. For example, the element in the first row and first column of BA is calculated as: $B[1,1]*A[1,1]+B[1,2]*A[2,1]$. Repeat this for all elements to fill the 4x4 matrix.

Key Concepts

Matrix Multiplication

Matrix multiplication involves multiplying rows of the first matrix by columns of the second matrix and summing the products. The number of columns in the first matrix must equal the number of rows in the second matrix for the product to be defined.

Dimension Compatibility

For two matrices A and B, the product AB is defined only if the number of columns in A equals the number of rows in B. Similarly, BA is defined only if the number of columns in B equals the number of rows in A.

Non-Commutativity of Matrix Multiplication

Matrix multiplication is generally not commutative, meaning AB does not necessarily equal BA. Both products may exist or only one may be defined, and their results can be different matrices.