Solve each equation using the quadratic formula. (1/2)x² + (1/4)x - 3 = 0

Solve each equation using the quadratic formula. (2/3)x² + (1/4)x = 3

Solve each equation for the specified variable. (Assume no denominators are 0.) F = kMv²/r , for v

For each equation, solve for x in terms of y. 4x² - 2xy + 3y² = 2

For each equation, solve for x in terms of y. 2x² + 4xy - 3y² = 2

Evaluate the discriminant for each equation. Then use it to determine the number of distinct solutions, and tell whether they are rational, irrational, or nonreal complex numbers. (Do not solve the equation.) x² - 8x + 16 = 0

Evaluate the discriminant for each equation. Then use it to determine the number of distinct solutions, and tell whether they are rational, irrational, or nonreal complex numbers. (Do not solve the equation.) 3x² + 5x + 2 = 0

Evaluate the discriminant for each equation. Then use it to determine the number of distinct solutions, and tell whether they are rational, irrational, or nonreal complex numbers. (Do not solve the equation.) 4x² = -6x + 3

Answer each question. Find the values of a, b, and c for which the quadratic equation. ax² + bx + c = 0 has the given numbers as solutions. (Hint: Use the zero-factor property in reverse.) i, -i

Use the following facts. If x represents an integer, then x+1 represents the next consecutive integer. If x represents an even integer, then x+2 represents the next consecutive even integer. If x represents an odd integer, then x+2 represents the next consecutive odd integer. Find two consecutive integers whose product is 110.

Use the following facts. If x represents an integer, then x+1 represents the next consecutive integer. If x represents an even integer, then x+2 represents the next consecutive even integer. If x represents an odd integer, then x+2 represents the next consecutive odd integer. Find two consecutive even integers whose product is 168.

Use the following facts. If x represents an integer, then x+1 represents the next consecutive integer. If x represents an even integer, then x+2 represents the next consecutive even integer. If x represents an odd integer, then x+2 represents the next consecutive odd integer. Find two consecutive even integers whose product is 224.

Use the following facts. If x represents an integer, then x+1 represents the next consecutive integer. If x represents an even integer, then x+2 represents the next consecutive even integer. If x represents an odd integer, then x+2 represents the next consecutive odd integer. Find two consecutive odd integers whose product is 63.

Use the following facts. If x represents an integer, then x+1 represents the next consecutive integer. If x represents an even integer, then x+2 represents the next consecutive even integer. If x represents an odd integer, then x+2 represents the next consecutive odd integer. Find two consecutive odd integers whose product is 143.

Use the following facts. If x represents an integer, then x+1 represents the next consecutive integer. If x represents an even integer, then x+2 represents the next consecutive even integer. If x represents an odd integer, then x+2 represents the next consecutive odd integer. The sum of the squares of two consecutive odd integers is 202. Find the integers.

Use the following facts. If x represents an integer, then x+1 represents the next consecutive integer. If x represents an even integer, then x+2 represents the next consecutive even integer. If x represents an odd integer, then x+2 represents the next consecutive odd integer. The sum of the squares of two consecutive even integers is 52. Find the integers.

Use the following facts. If x represents an integer, then x+1 represents the next consecutive integer. If x represents an even integer, then x+2 represents the next consecutive even integer. If x represents an odd integer, then x+2 represents the next consecutive odd integer. The difference of the squares of two positive consecutive even integers is 84. Find the integers.

Use the following facts. If x represents an integer, then x+1 represents the next consecutive integer. If x represents an even integer, then x+2 represents the next consecutive even integer. If x represents an odd integer, then x+2 represents the next consecutive odd integer. The difference of the squares of two positive consecutive odd integers is 32. Find the integers.

Dimensions of a Square. The length of each side of a square is 3 in. more than the length of each side of a smaller square. The sum of the areas of the squares is 149 in.². Find the lengths of the sides of the two squares.

Dimensions of a Parking Lot. A parking lot has a rectangular area of 40,000 yd². The length is 200 yd more than twice the width. Find the dimensions of the lot.

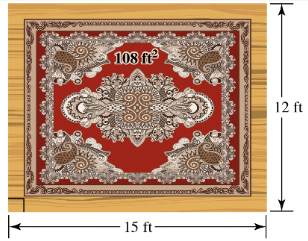
Dimensions of a Rug. Zachary wants to buy a rug for a room that is 12 ft wide and 15 ft long. He wants to leave a uniform strip of floor around the rug. He can afford to buy 108 ft² of carpeting. What dimensions should the rug have?

Volume of a Box. A rectangular piece of metal is 10 in. longer than it is wide. Squares with sides 2 in. long are cut from the four corners, and the flaps are folded upward to form an open box. If the volume of the box is 835 in.³, what were the original dimensions of the piece of metal?

Manufacturing to Specifications. A manufacturing firm wants to package its product in a cylindrical container 3 ft high with surface area 8π ft². What should the radius of the circular top and bottom of the container be? (Hint: The surface area consists of the circular top and bottom and a rectangle that represents the side cut open vertically and unrolled.)

Dimensions of a Square What is the length of the side of a square if its area and perimeter are numerically equal?

Radius of a Can A can of Blue Runner Red Kidney Beans has surface area 371 cm². Its height is 12 cm. What is the radius of the circular top? Round to the nearest hundredth.

Length of a Walkway A nature conservancy group decides to construct a raised wooden walkway through a wetland area. To enclose the most interesting part of the wetlands, the walkway will have the shape of a right triangle with one leg 700 yd longer than the other and the hypotenuse 100 yd longer than the longer leg. Find the total length of the walkway.

Height of a Projectile A projectile is launched from ground level with an initial velocity of v₀ feet per second. Neglecting air resistance, its height in feet t seconds after launch is given by s=-16t²+v₀t. In each exercise, find the time(s) that the projectile will (a) reach a height of 80 ft and (b) return to the ground for the given value of v₀. Round answers to the nearest hundredth if necessary. v₀=96

Height of a Projectile A projectile is launched from ground level with an initial velocity of v₀ feet per second. Neglecting air resistance, its height in feet t seconds after launch is given by s=-16t²+v₀t. In each exercise, find the time(s) that the projectile will (a) reach a height of 80 ft and (b) return to the ground for the given value of v₀. Round answers to the nearest hundredth if necessary. v₀=32

Height of a Projected Ball An astronaut on the moon throws a baseball upward. The astronaut is 6 ft, 6 in. tall, and the initial velocity of the ball is 30 ft per sec. The height s of the ball in feet is given by the equations=-2.7t²+30t+6.5,where t is the number of seconds after the ball was thrown. (a) After how many seconds is the ball 12 ft above the moon's surface? Round to the nearest hundredth. (b) How many seconds will it take for the ball to hit the moon's surface? Round to the nearest hundredth.

Match each equation in Column I with the correct first step for solving it in Column II. √(x+5) = 7