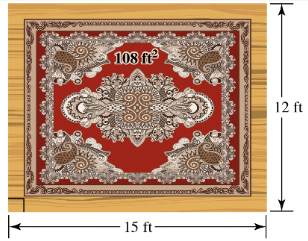
Dimensions of a Rug. Zachary wants to buy a rug for a room that is 12 ft wide and 15 ft long. He wants to leave a uniform strip of floor around the rug. He can afford to buy 108 ft² of carpeting. What dimensions should the rug have?

Verified step by step guidance

1. Let the width of the uniform strip around the rug be represented by \(x\) feet. Since the room is 12 ft wide and 15 ft long, the dimensions of the rug will be reduced by \$2x\( on each side, making the rug's width \)(12 - 2x)\( and length \)(15 - 2x)$.
2. Write an expression for the area of the rug in terms of \(x\): \(\text{Area} = (12 - 2x)(15 - 2x)\).
3. Set the area expression equal to the amount of carpeting Zachary can afford, which is 108 square feet: \((12 - 2x)(15 - 2x) = 108\).
4. Expand the left side of the equation to form a quadratic equation: \$180 - 24x - 30x + 4x^2 = 108$.
5. Simplify and rearrange the quadratic equation to standard form: \$4x^2 - 54x + 72 = 0\(. Then, solve for \)x$ using the quadratic formula or factoring to find the width of the strip, and subsequently find the rug's dimensions.

Key Concepts

Area of a Rectangle

The area of a rectangle is found by multiplying its length by its width. In this problem, both the room and the rug are rectangular, so understanding how to calculate area is essential to relate the rug's dimensions to the amount of carpeting Zachary can afford.

Uniform Strip Around the Rug

A uniform strip means the rug is placed so that the distance from the rug's edges to the room's walls is the same on all sides. This concept helps set up expressions for the rug's length and width in terms of the strip width, which is key to forming an equation.

Forming and Solving Quadratic Equations

Setting up the rug's area as a function of the strip width leads to a quadratic equation. Solving this equation allows us to find the strip width and thus the rug's dimensions. Understanding how to form and solve quadratics is crucial for finding the correct solution.