Hey, everyone. We've worked with some basic graphs of functions and here we're going to focus on one specific type of function, the quadratic function. Now it might seem like a lot of information at first and this graph behind me might look a little bit intimidating but don't worry, I'm going to walk you through absolutely everything that you need to know about the graphs of quadratic functions here and you'll be an expert in no time. So let's go ahead and jump right in.
So a quadratic function is a polynomial of degree 2 that has a standard form of \( f(x) = ax^2 + bx + c \). All of these functions here are examples of quadratic functions and you can see that a, b, and c can be any real number, whether it be a fraction, a negative number, or even 0, so long as \( a \neq 0 \) and our largest exponent is still 2, making it a quadratic function.
Now here we're going to focus on the graphs of quadratic functions so let's go ahead and take a look here. Now we've worked with the square function before \( f(x) = x^2 \) and you may remember that this square function was a parabola. This is actually going to be the same for all quadratic functions. They are all going to have this curved parabolic shape. Whether it is right side up, upside down, or located anywhere on our coordinate plane, our quadratic functions will always be that same shape of a parabola.
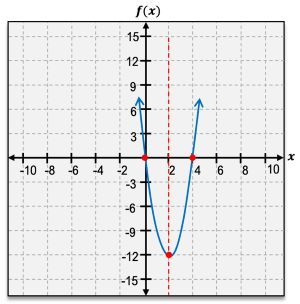
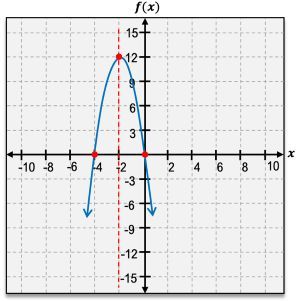
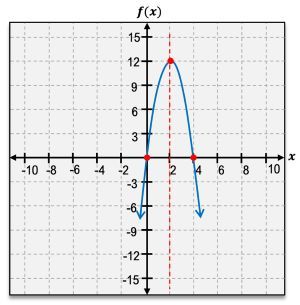
So we're going to look at the different elements of a parabola here and some are going to be the ones that we're familiar with, like the x intercept or the y intercept, but we're also going to work with some that are specific to parabolas, like the vertex or the axis of symmetry. So let's go ahead and get started with our vertex. The vertex of a parabola is either going to be the lowest point or the highest point depending on whether our parabola is opening upward or opening downward.
So for our square function here, we see that our vertex is right at that origin point and we're always going to write our vertex as an ordered pair, so my vertex is simply (0, 0). Now for my other function here, it is not at the origin, it is actually at the point (-2, 1), so my vertex is (-2, 1). The other thing that I want to consider with my vertex is whether I'm dealing with a minimum or a maximum point.
So again looking at my square function here, this is the lowest point on my graph of that quadratic function. So it is a minimum point. It's all the way at the bottom and nothing goes below it on that parabola. So not only is my vertex here (0, 0), it also represents a minimum. Now for my other function, my vertex is all the way at the top, which tells me that I am not dealing with a minimum. I'm actually dealing with a maximum point here. So here, my vertex is (-2, 1), and it is a maximum.
Now let's go ahead and look at my x intercept. The x intercept of a graph is anywhere that our graph crosses our x axis. And between my two functions here, I have three different points that cross my x axis that represent my x intercepts. So let's take a look at our square function. Now there's only one point that crosses the x axis and it is at my origin. So my x intercept is simply \(0\). Now looking at my other function, there are two points that cross the x axis, so I need to account for both of them, -3 and -1, as my x intercepts.
Now let's move on to our y intercept. The y intercept is where a graph crosses the y axis. So let's look at our square function first. We have this point. This represents our y intercept. Now our y intercept here is again at the origin simply at \(0\). And for my other graph, my other function, my y intercept is down here at -3, so it's simply \(y = -3\).
Now we've looked at our intercepts and our vertex. Now we want to look at our axis of symmetry. Our axis of symmetry is going to be specific to parabolas and it represents the line that divides our parabola perfectly in half. It is symmetric about that line. So our axis of symmetry is going to perfectly cut it in half. So looking at my square function, it's going to go straight through the middle and it's actually always going to go straight through our vertex. So here my axis of symmetry is simply the line \(x = 0\), a vertical line through my vertex.
Now looking at our other function here, if I draw a line that divides this perfectly in half, you're often going to see this actually written with a dotted line but I've just highlighted them here so that it's easier to see. But here again we're going straight through that vertex point at \(x = -2\). So it's always going to be a straight vertical line through our vertex, and that represents our axis of symmetry. If I were to fold my parabola in half at that line, it's going to perfectly match up because it is symmetric about that line.
Somet