Graph each polynomial function. ƒ(x)=-2x4+7x3-4x2-4x
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
4. Polynomial Functions
Understanding Polynomial Functions
Problem 55
Textbook Question
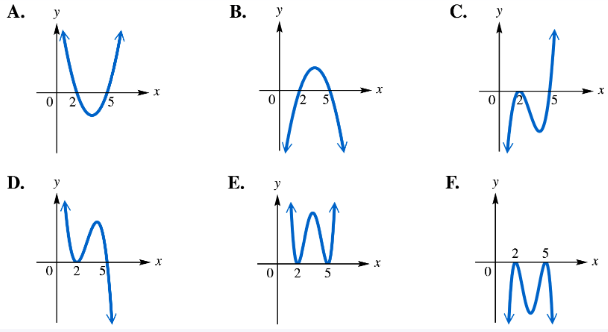
For each polynomial function, identify its graph from choices A–F. ƒ(x)=(x-2)2(x-5)2
 Verified step by step guidance
Verified step by step guidance1
Start by identifying the zeros of the polynomial function ƒ(x) = (x-2)^2 (x-5)^2. The zeros are the values of x that make the function equal to zero. Set each factor equal to zero: x - 2 = 0 and x - 5 = 0, so the zeros are x = 2 and x = 5.
Next, determine the multiplicity of each zero. Since both factors are squared, each zero has multiplicity 2. This means the graph will touch the x-axis at these points but will not cross it.
Analyze the end behavior of the polynomial. Since the polynomial is the product of two squared binomials, its degree is 4 (2 + 2), which is even, and the leading coefficient is positive (since the leading terms multiply to a positive x^4 term). Therefore, as x approaches ±∞, ƒ(x) approaches +∞.
Use the information about zeros and end behavior to match the graph: the graph should touch the x-axis at x=2 and x=5 without crossing, and both ends of the graph should rise upwards.
Finally, compare these characteristics with the given graph choices A–F to identify which graph matches the zeros, multiplicities, and end behavior described.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
8mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Polynomial Functions and Their Graphs
Polynomial functions are expressions involving variables raised to whole-number exponents combined using addition, subtraction, and multiplication. Their graphs are smooth and continuous curves, with shapes influenced by the degree and coefficients of the polynomial. Understanding the general shape helps in matching the function to its graph.
Recommended video:

Graphing Polynomial Functions
Zeros and Their Multiplicities
The zeros of a polynomial are the values of x that make the function equal to zero. The multiplicity of a zero indicates how many times that root is repeated. Even multiplicities cause the graph to touch the x-axis and turn around, while odd multiplicities cause the graph to cross the axis.
Recommended video:

Finding Zeros & Their Multiplicity
End Behavior of Polynomial Functions
The end behavior describes how the graph behaves as x approaches positive or negative infinity. It depends on the leading term's degree and coefficient. For even-degree polynomials with positive leading coefficients, both ends rise; for even degree with negative coefficients, both ends fall.
Recommended video:

End Behavior of Polynomial Functions

 6:04m
6:04mWatch next
Master Introduction to Polynomial Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
792
views
