Identify the ordered pair of the vertex of the parabola. State whether it is a minimum or maximum.

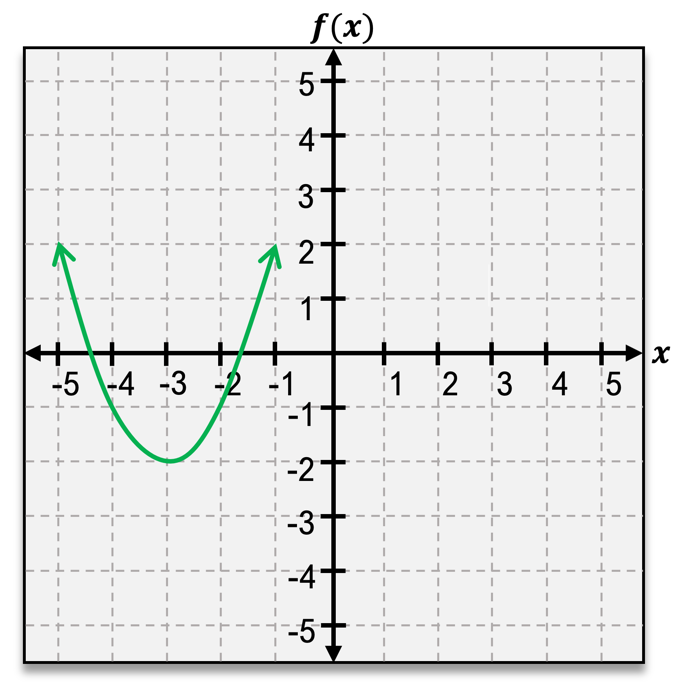
• A. $\left(-3,-2\right);$ maximum
• B. $\left(-3,-2\right);$ minimum
• C. $\left(-1,2\right);$ maximum
• D. $\left(-1,2\right);$ minimum

Answer: (B)

Verified step by step guidance

1. Observe the graph of the parabola. It opens upwards, indicating that the vertex is a minimum point.
2. Identify the vertex of the parabola on the graph. The vertex is the lowest point on the graph.
3. Locate the coordinates of the vertex. From the graph, the vertex is at the point (-3, -2).
4. Since the parabola opens upwards, the vertex represents a minimum value of the function.
5. Conclude that the ordered pair of the vertex is (-3, -2) and it is a minimum.