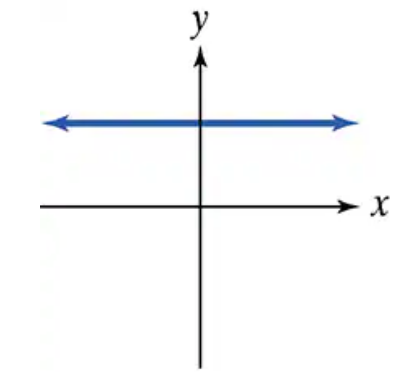
Use the vertical line test to identify graphs in which y is a function of x.

Verified step by step guidance

1. Step 1: Understand the vertical line test. The vertical line test is a method used to determine if a graph represents a function. If any vertical line intersects the graph at more than one point, then the graph does not represent a function.
2. Step 2: Observe the graph provided. The graph shows a red curve plotted on a grid with x and y axes labeled. The curve appears to loop and extend outward.
3. Step 3: Apply the vertical line test. Imagine drawing vertical lines at various x-values across the graph. Check if any vertical line intersects the red curve at more than one point.
4. Step 4: Analyze intersections. For this graph, vertical lines drawn at certain x-values (e.g., near x = 0) will intersect the curve at two points, indicating that the graph fails the vertical line test.
5. Step 5: Conclude. Since some vertical lines intersect the graph at more than one point, the graph does not represent y as a function of x.

Key Concepts

Function Definition

A function is a relation between a set of inputs and a set of possible outputs where each input is related to exactly one output. In mathematical terms, for every x-value in the domain, there is a unique y-value in the range. This concept is fundamental in determining whether a graph represents a function.

Vertical Line Test

The vertical line test is a method used to determine if a graph represents a function. If any vertical line drawn through the graph intersects it at more than one point, the graph does not represent a function. This test visually confirms the uniqueness of y-values for each x-value.

Graph Interpretation

Interpreting graphs involves understanding the relationship between the x and y coordinates represented visually. It requires analyzing the shape, direction, and intersections of the graph to determine properties such as continuity, limits, and whether it meets the criteria of a function as defined by the vertical line test.