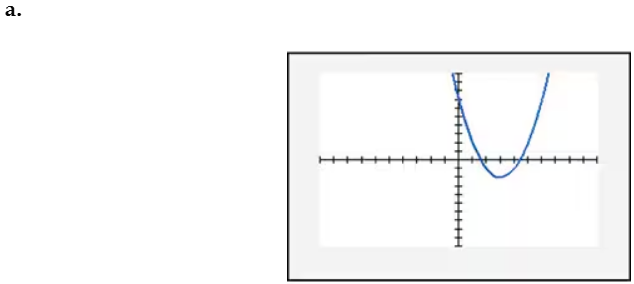
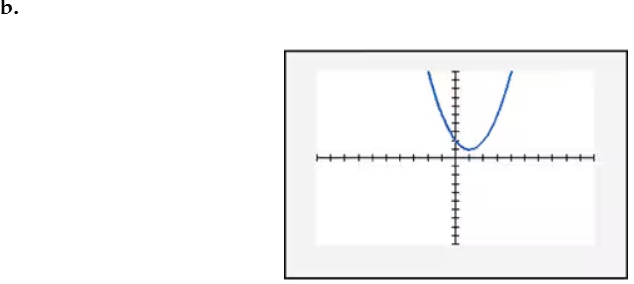
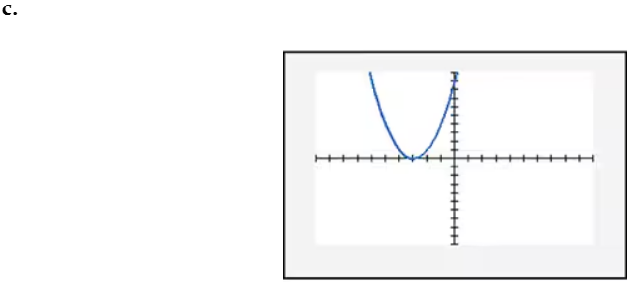
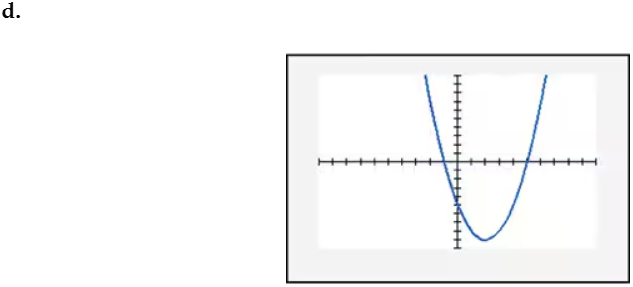
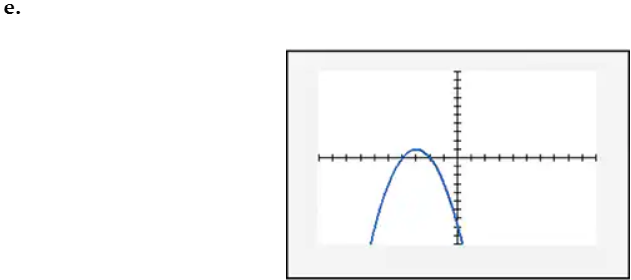
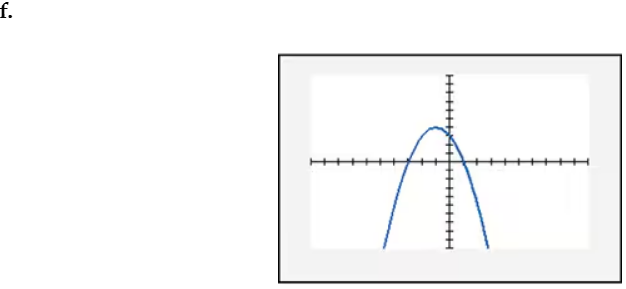
In Exercises 109–114, find the x-intercept(s) of the graph of each equation. Use the x-intercepts to match the equation with its graph. The graphs are shown in [- 10, 10, 1] by [- 10, 10, 1] viewing rectangles and labeled (a) through (f). y = x² - 2x + 2

Verified step by step guidance

1. To find the x-intercepts of the graph of the equation \( y = x^2 - 2x + 2 \), set \( y = 0 \). This is because the x-intercepts occur where the graph crosses the x-axis, and at these points, the value of \( y \) is zero.
2. The equation becomes \( 0 = x^2 - 2x + 2 \). This is a quadratic equation, so we will solve it using the quadratic formula: \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \), where \( a \), \( b \), and \( c \) are the coefficients from the standard form of the quadratic equation \( ax^2 + bx + c = 0 \).
3. Identify the coefficients: \( a = 1 \), \( b = -2 \), and \( c = 2 \). Substitute these values into the quadratic formula: \( x = \frac{-(-2) \pm \sqrt{(-2)^2 - 4(1)(2)}}{2(1)} \).
4. Simplify the discriminant (the expression under the square root): \( (-2)^2 - 4(1)(2) = 4 - 8 = -4 \). Since the discriminant is negative, the equation has no real solutions, meaning the graph does not cross the x-axis. Instead, the solutions are complex numbers.
5. Conclude that the graph of \( y = x^2 - 2x + 2 \) has no x-intercepts. This means the parabola does not intersect the x-axis, and its vertex lies above the x-axis because the parabola opens upwards (as \( a > 0 \)).

Key Concepts

X-Intercept

The x-intercept of a graph is the point where the graph intersects the x-axis. This occurs when the value of y is zero. To find the x-intercept(s) of an equation, you set y equal to zero and solve for x. In the context of the given equation, this means solving the quadratic equation x^2 - 2x + 2 = 0.

Quadratic Equations

A quadratic equation is a polynomial equation of the form ax^2 + bx + c = 0, where a, b, and c are constants, and a is not zero. The solutions to a quadratic equation can be found using various methods, including factoring, completing the square, or applying the quadratic formula. Understanding the nature of the roots (real or complex) is essential for determining the x-intercepts.

Graphing Quadratics

Graphing a quadratic function involves plotting a parabola, which can open upwards or downwards depending on the sign of the leading coefficient (a). The vertex of the parabola represents the maximum or minimum point, and the x-intercepts indicate where the graph crosses the x-axis. Analyzing the graph helps in visualizing the solutions and understanding the behavior of the function.